Funciones trigonométricas
Las funciones están en muchos ámbitos de la vida. Por ejemplo, el movimiento oscilatorio de este gato se puede representar a través de una función.

¿Cómo podemos representarlo? A través de funciones trigonométricas. ¡Vamos a ver cómo son cada una!
Función Seno
En trigonometría, el seno de un ángulo de un triángulo rectángulo se define como la razón entre el cateto opuesto de dicho ángulo y la hipotenusa. Si tenemos una circuferencia goniométrica (es decir, la circunferencia de radio 1) se tiene que:
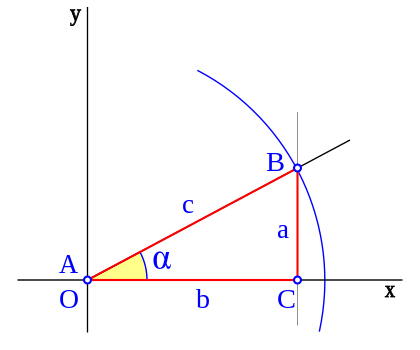
Vamos a representar ahora la función seno. Para ello, gira el punto B sobre la circunferencia goniométrica.
Ayudándote del dibujo de la función, para , ¿cuánto vale seno de alfa?
Función coseno
En trigonometría, el coseno de un ángulo de un triángulo rectángulo se define como la razón entre el cateto adyacente a dicho ángulo y la hipotenusa.
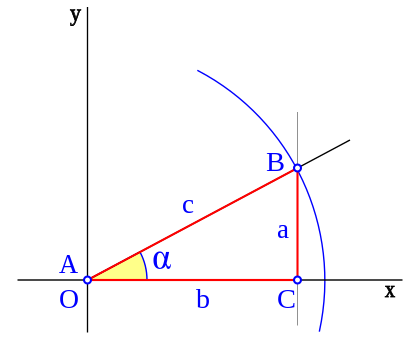
Si B pertenece a la circunferencia goniométrica se tiene que:
Vamos a representar ahora la función coseno. Para ello, gira el punto B sobre la circunferencia goniométrica.
Ayudándote del dibujo de la función, para , ¿cuánto vale coseno de alfa?
Función Tangente
En trigonometría, la tangente de un ángulo de un triángulo rectángulo se define como el cociente entre el cateto opuesto y el adyacente.
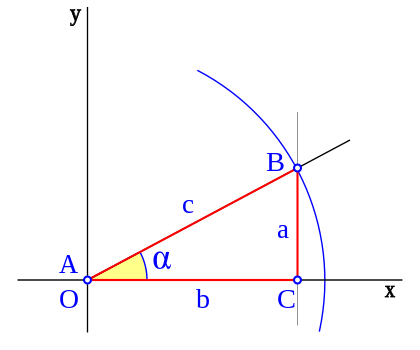
Vamos a representar ahora la función tangente. Para ello, gira el punto B sobre la circunferencia goniométrica.
Ayudándote del dibujo de la función, para , ¿cuánto vale tangente de alfa?
Funciones trigonométricas
Vamos a repasar cada una de las funciones que hemos visto, juntándolas todas en una misma gráfica.
¿Cómo podemos representar un movimiento como el del gato?
Muy sencillo, a través de la función coseno.
La trayectoria de la bola de un péndulo simple sigue la siguiente fórmula:
Siendo: , el máximo desplazamiento angular del péndulo; T, el periodo; t, el tiempo.
Por otro lado, T depende de la longitud de la cuerda del péndulo y de la aceleración de la gravedad:
¡Vamos a representarlo!