Google Classroom
GeoGebraGeoGebra Klaslokaal
GeoGebra

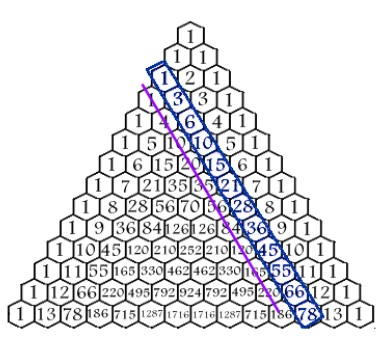
Getalpatronen in De Driehoek van Pascal

Auteur:m.jacobs, Jan Elemans

Driehoeksgetallen

Op onderstaande foto zie je een bouwwerk van sneeuwballen bestaande uit vier lagen.
Image

Vraag 1

Is dit een piramide?

Vink alles aan wat van toepassing is
  • A
  • B
Controleer mijn antwoord (3)

Vraag 2

Waarom wel/niet?

Controleer mijn antwoord

Vraag 3

Uit hoeveel sneeuwballen bestaat dit bouwwerk?

Controleer mijn antwoord

Vraag 4

Hoeveel sneeuwballen zitten er in elke laag? Geef antwoord op vraag a, b, c en d hieronder. Tel vanaf de top van het bouwwerk, we noemen dus de bovenste laag laag 1.
Image

Vraag a

Welk getal komt er in de tabel op de plaats van (a)?

Controleer mijn antwoord

Vraag b

Welk getal komt er in de tabel op de plaats van (b)?

Controleer mijn antwoord

Vraag c

Welk getal komt er in de tabel op de plaats van (c)?

Controleer mijn antwoord

Vraag d

Welk getal komt er in de tabel op de plaats van (d)?

Controleer mijn antwoord

Driehoeksgetallen

Deze getallen zijn voorbeelden van figurale getallen, omdat je er een bepaald figuur van kan maken. Omdat de sneeuwballen steeds met elkaar een driehoek vormen, noemen we deze getallen driehoeksgetallen. Elke laag van het bouwwerk stelt dus een driehoeksgetal voor.

Vraag 5

Stel dat we het sneeuwballen bouwwerk groter zouden willen maken en we leggen er een laag onder, uit hoeveel sneeuwballen zou laag 5 dan bestaan?

Controleer mijn antwoord

Vraag 6

Vraag 6

In de tabel hierboven zie je de eerste 5 driehoeksgetallen. Vul deze rij aan met de volgende vijf getallen, waarbij n het nummer van het driehoeksgetal aangeeft. Typ tussen de getallen steeds een komma gevolgd door een spaties om de getallen te scheiden. Voor de eerste vijf getallen zou dat er zo uit zien: 1, 3, 6, 10, 15 Begin met het zesde driehoeksgetal.

Controleer mijn antwoord

Vraag 7

Welke regelmaat kun je ontdekken in de tabel?

Controleer mijn antwoord

Carl Friedrich Gauss

Carl Friedrich Gauss (1777-1855) was een Duitse wis- en natuurkundige, die een zeer belangrijke bijdrage heeft geleverd aan een groot aantal deelgebieden van de wiskunde (en de exacte wetenschappen), waaronder de getaltheorie. We gaan kijken hoe je gemakkelijk de getallen 1 t/m 100 bij elkaar op kunt tellen.

Vraag 8a

Tel de getallen 1 t/m 10 bij elkaar op, hoeveel komt daaruit? Vul dus het antwoord in van: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 =

Controleer mijn antwoord

Vraag 8b

Waar heb je deze uitkomst eerder gezien? Waar is deze uitkomst dus gelijk aan?

Controleer mijn antwoord

Gauss' geweldige truc voor driehoeksgetallen

We gaan nu kijken naar een filmpje waarin driehoeksgetallen gebruikt worden om snel de som te bepalen van de getallen 1 t/m 100. Hier laat men zien hoe Gauss als zevenjarig jongetje heeft bedacht om heel snel opeenvolgende getallen bij elkaar op te tellen. Begrijp je de truc? En herken je de driehoeksgetallen?

Blaise Pascal

Al ver voordat Gauss geboren was, leefde Blaise Pascal, hij was een Franse wis- en natuurkundige in de 17e eeuw (1623-1662). Hij bouwde o.a. één van de eerste mechanische rekenmachines en had een belangrijke bijdrage in de combinatoriek (ook wel de kunst van het tellen genoemd). Zo bedacht hij een handige manier om routes in een rooster te tellen waarmee de Driehoek van Pascal ontstond. In deze driehoek zijn heel veel patronen van getallen te ontdekken. We gaan een heel klein tipje van de sluier oplichten.

Driehoek van Pascal

Via handig tellen kun je bepalen op hoeveel manieren je vanuit Start (via de kortste weg) naar een punt in dit rooster kunt lopen. In de volgende vragen ga je ontdekken hoe. Begin met het beantwoorden van vraag 9.

Vraag 9

Klik in de app hierboven op Reset en daarna drie keer op >. Je krijgt dan onderstaand figuur.
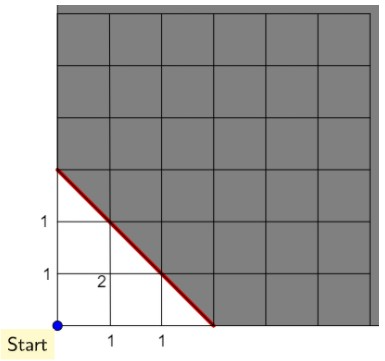
Image

Kun je nu zelf uitrekenen op hoeveel manieren je bij de snijpunten van de roosterlijnen met de rode lijn kunt komen, steeds via de kortste weg? Hoe kun je dus steeds het volgende getal vinden?

Controleer mijn antwoord

Vraag 10

Welke getallen komen er nu bij de snijpunten met de rode lijn te staan? Typ tussen de getallen steeds een komma gevolgd door een spaties om de getallen te scheiden.

Controleer mijn antwoord

Vraag 11

Controleer de antwoorden van vraag 9 en 10 met de applet door steeds op > te klikken. Had je dit systeem ook bedacht?

Driehoek van Pascal anders vorm gegeven

Wanneer je de driehoek van Pascal een kwartslag draait kun je ervoor zorgen dat het startpunt bovenaan komt te liggen. Dat ziet er zo uit:
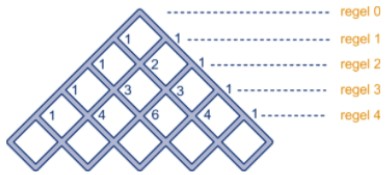
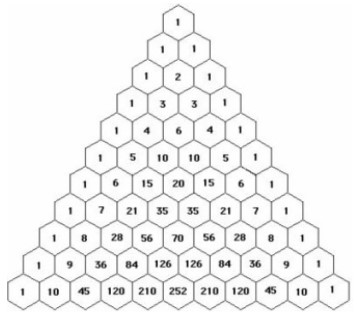
Image
Of zo (merk op: de hoekpunten van de vierkanten in de vorige figuur zijn nu steeds het middelpunt van een zeshoek):
Image

Vraag 12 Waar bevinden zich de driehoeksgetallen?

Herken je de driehoeksgetallen in de Driehoek van Pascal hierboven? (Controleer je antwoord in de figuur onderaan dit werkblad bij oplossing 1.)

Piramidegetallen (m.b.v. driehoeken)

We begonnen de les met een piramide van sneeuwballen en hebben toen het aantal sneeuwballen per laag bekeken. Nu gaan we eens kijken naar het totaal aantal sneeuwballen per piramide. We gaan weer uit van een piramide met een driehoek als grondvlak (met andere woorden elke laag van de piramide bestaat uit een driehoek van sneeuwballen).

Vraag 13

Zie de tabel hieronder.
Image

Vraag a

Welk getal komt er in de tabel op de plaats van (a)?

Controleer mijn antwoord

Vraag b

Welk getal komt er in de tabel op de plaats van (b)?

Controleer mijn antwoord

Vraag c

Welk getal komt er in de tabel op de plaats van (c)?

Controleer mijn antwoord

Vraag d

Welk getal komt er in de tabel op de plaats van (d)?

Controleer mijn antwoord

Vraag e

Welk getal komt er in de tabel op de plaats van (e)?

Controleer mijn antwoord

Vraag 14

Welke regelmaat kun je hier ontdekken?

Controleer mijn antwoord

Vraag 15

Waar zie je deze piramidegetallen terug in de Driehoek van Pascal? (Controleer je antwoord onderaan het werkblad bij oplossing 2.)

Vraag 16

Wat is dus het 10e piramidegetal?

Controleer mijn antwoord

Oplossing 1: Driehoeksgetallen in De Driehoek van Pascal.

Oplossing 1: Driehoeksgetallen in De Driehoek van Pascal.

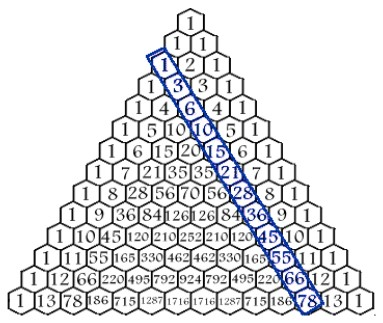
Oplossing 2: Piramidegetallen in De Driehoek van Pascal

De piramidegetallen liggen allen op de schuine lijn direct links van de driehoeksgetallen (je telt dus steeds een driehoeksgetal op bij het vorige piramidegetal). Zie de paarse lijn in de onderstaande Driehoek van Pascal.
Image

Nieuw didactisch materiaal

Ontdek materiaal

Ontdek onderwerpen