Contenu
Johnson lichamen
Naast de Platonische lichamen en de Archimedische lichamen bestaat er nog een heel aparte en omvangrijke groep van Johnson lichamen. Het zijn er niet minder dan 92 en ze werden pas in 1966 opgelijst en genummerd.
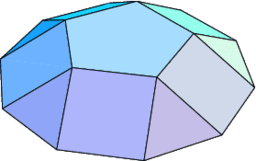
Table des matières
wat zijn Johnson lichamen
piramiden, koepels en rotonden
getransformeerde piramiden en bipiramiden
getransformeerde koepels en rotonden
- transformaties van koepels en rotonden
- J18 verlengde driehoekige koepel
- J19 verlengde vierkante koepel
- J20 verlengde vijfhoekige koepel
- J21 verlengde vijfhoekige rotonde
- J22 verlengde gedraaide driehoekige koepel
- J23 verlengde gedraaide vierkante koepel
- J24 verlengde gedraaide vijfhoekige koepel
- J25 verlengde gedraaide vijfhoekige rotonde
- J26 gyrobifastigium
- J27 driehoekige dubbelkoepel
- J28 vierkante dubbelkoepel
- J29 gedraaide vierkante dubbelkoepel
- J30 vijfhoekige dubbelkoepel
- J31 gedraaide vijfhoekige dubbelkoepel
- J32 vijfhoekige koepelrotonde
- J33 gedraaide vijfhoekige koepelrotonde
- J34 vijfhoekige dubbelrotonde
verlengde dubbelkoepels en -rotonden
- verlengde dubbelkoepels en -rotonden
- J35 verlengde driehoekige dubbelkoepel
- J36 verlengde gedraaide driehoekige dubbelkoepel
- J37 verlengde gedraaide vierkante dubbelkoepel
- J38 verlengde vijfhoekige dubbelkoepel
- J39 verlengde gedraaide vijfhoekige dubbelkoepel
- J40 verlengde vijfhoekige koepelrotonde
- J41 verlengde gedraaide vijfhoekige koepelrotonde
- J42 verlengde vijfhoekige dubbelrotonde
- J43 verlengde gedraaide vijfhoekige dubbelrotonde
- J44 verlengde dubbelgedraaide 3h. dubbelkoepel
- J45 verlengde gedraaide vierkante dubbelkoepel
- J46 verlengde dubbelgedraaide vijfhoekige dubbelkoepel
- J47 verlengde dubbelgedraaide vijfhoekige koepelrotonde
- J48 verlengde dubbelgedraaide vijfhoekige dubbelrotonde
verhoogde prisma's
- J49 verhoogd driehoekig prisma
- J50 dubbelverhoogd driehoekig prisma
- J51 drievoudig verhoogd driehoekig prisma
- J52 verhoogd vijfhoekig prisma
- J53 dubbelverhoogd vijfhoekig prisma
- J54 verhoogd zeshoekig prisma
- J55 paradubbelverhoogd zeshoekig prisma
- J56 metadubbelverhoogd zeshoekig prisma
- J57 drievoudig verhoogd zeshoekig prisma
getransformeerde platonische lichamen
getransformeerde archimedische lichamen
- J65 verhoogde afgeknotte tetraëder
- J66 verhoogde afgeknotte kubus
- J67 dubbelverhoogde afgeknotte kubus
- J68 verhoogde afgeknotte dodecaëder
- J69 paradubbelverhoogde afgeknotte dodecaëder
- J70 metadubbelverhoogde afgeknotte dodecaëder
- J71 driedubbelverhoogde afgeknotte dodecaëder
- J72 gedraaide rombische icosidodecaëder
- J73 paradubbelgedraaide rombische icosidodecaëder
- J74 metadubbelgedraaide rombische icosidodecaëder
- J75 drievoudig gedraaide rombische icosidodecaëder
- J76 verkleinde rombische icosidodecaëder
- J77 paragedraaide verkleinde rombische icosidodecaëder
- J78 metagedraaide verkleinde rombische icosidodecaëder
- J79 dubbelgedraaide verkleinde rombische icosidodecaëder
- J80 paradubbelverkleinde rombische icosidodecaëder
- J81 metadubbelverkleinde rombische icosidodecaëder
- J82 gedraaide dubbelverkleinde rombische icosidodecaëder
- J83 drievoudig verkleinde rombische icosidodecaëder
overige lichamen