perpendicular lines to an oval and an ellipse
perpendicular lines to an oval
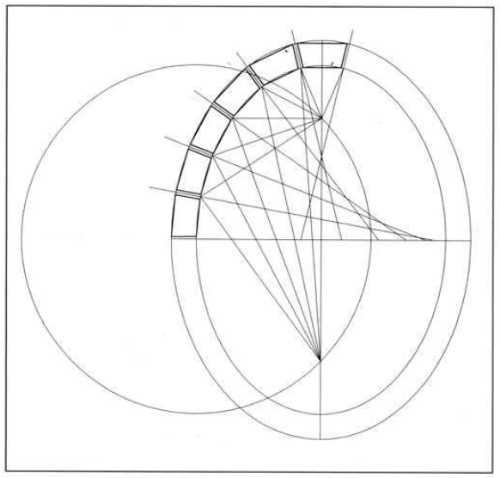
In his article Ellissi e ovali, epilogo di un conflitto Riccardo Miglari further comments the difference between the shape of ovals and ellipses op het vormverschil tussen ovaal en ellips. An oval is a concatenation of circular arcs. So perpendicular lines drawn from the circumference of an oval run through the centers of these circular arcs.
perpendicular lines to an ellipse
Bur an ellipse is isn't a concatenation of circular arcs. More, the ellipse is is a curve whose curvature is changing continuously. The consequence is that perpendicular lines to an ellipse are not concurrent.
When drawing a serie of perpendicular lines to an ellips you'll see a flat curve: the evolute of the ellipse.
curvature
Ovals not only are easier to draw, they also are uch more practicle in architactural use.
- If you want to surround a square by a colonnade, you have to construct the normals to a curve. For an oval is this is not a problem, since all radii of a circle ru through its center. However for an you have to construct each normal one by one.
- If you want to realise an ellipse in cut stones, you will have to give each stone a different shape because each point of the ellipse has got a different curvature while a oval has got a constant curvature
Precisely the curvature is a feature that makes you recognise the difference between oval and ellipse. A skilled eye recognises an oval havinf 4 (of more) points where the curvature changes.
But for historical monuments this isn't always easy. You can't build a dome without any inaccuracy and withing time differences can occur due to setting of the building. Put this next to the little difference between oval and ellipse and you'll soon realise that measuring doesn't solve the problem.
WIthout any knowledge of historical sources, architectural practice and -history indeed you get lost into abiguity and discussions on ovals and ellipses