Clothoids
Clothoid is the curve for smoothly transiting between different curvatures (straight line has zero curvature). In the figure below, the clothoid curve (red) bridges between two different curvatures represented by two osculating circles (blue). In the applet above, when "Tracing" is checked, all osculating circles are drawn and the clothoid curve will naturally emerge from that bundle of circles.
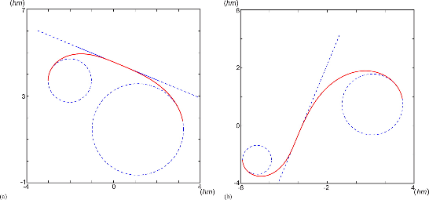
Here, "osculating" means "kissing", i.e. 2nd order tangent: while there are infinite many circles 1st-order tangent to a curve at a given point, there is only one 2nd-order tangent circle which defines the curvature at that point as reciprocal of the radius of that circle . The osculating circle with its center and radius are called circle of curvature, center of curvature and radius of curvature at that point.
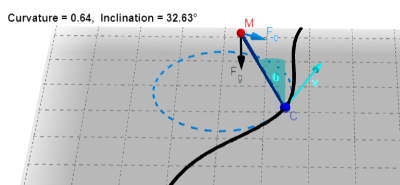
When a vehicle moves with velocity around the curvature , its centripetal acceleration is a vector toward the center of curvature and its passengers experience a centrifugal force in opposite direction.
When transiting between different curvatures, e.g. entering the turn from a straight road, in order to avoid shock due to sudden change of centrifugal force, we should change the curvature gradually and smoothly with a curvature function . The simplest curvature function a linear function connecting the curvatures & at two ends. The clothoid with this linear curvature function was studied first by Leonhard Euler (so named "Euler spiral"), then by Marie Alfred Cornu (so named "Cornu spiral"). After that, the name "clothoid" was coined by Ernesto Cesàro following the Greek mythological figure Clotho the spinner who is the first one in the Three Fates (Clotho spins the thread of life, Lachesis draws it out, Atropos cuts it).
Here, we consider generalized clothoids with arbitrary continuous curvature function (see the drop box "Curvature function" in the applet above):
- "Euler spiral": the original clothoid with linear curvature function.
- Extended meander curves: the family of clothoids generated by the sine curvature functions which resembles the meander of river. Their shape varies with two parameters ϕmax and ω. Here are some special cases: 1. When ϕmax=1, ω=0 ("Sinusoid" in the list), it resembles the sine curve itself, just a little bit blunter (check "Matching curve" to see it). 2. When ϕmax≈0.766π, ω=0 ("Meander curve" in the list with "Lemniscate (∞)" checked), it closes into a lemniscate (∞). 3. When ϕmax=-1.6π, ω=0.04π, it winds into a 5-petal flower.
- Asymmetric spirals: "Exp spiral" and "Lox spiral" are from exp() and ln() curvature functions.
- Centric spirals: "Log spiral" is exactly the equiangular logarithmic spiral; "Archimedean spiral" is the equidistant spiral slightly different from the standard one.
- And some demos of drawing by polynomial curvature functions.
Bonus:
Here is some interesting facts about clothoid.

When we peel an orange along an equidistant spiral (spherical Archimedean spiral) then flatten it out, we also receive a clothoid, as described in the paper Orange Peels and Fresnel Integrals.

That double spiral (clothoid) flattened out from spherical equidistant spiral is similar but not the same with the double spiral stereographically projected from spherical equiangular spiral (loxodrome, rhumb line) onto the plane which is a Möbius-transformed logarithmic spiral:
