高中常见读数方法及原理
一、刻度尺读数&读数一般性原则
首先,在介绍较为复杂的例如游标卡尺等工具原理之前,先让我们来重温一下最简单的刻度尺是怎么读数的。
这是一把普通的刻度尺的实物图。

从图中可以看出,该刻度尺的量程为15cm,最小分度值为0.1cm.(最小分度值就是在测量仪器所能读出的最小值,指测量工具上相邻的两个刻度之间的最小格的数值。)
我们怎么用刻度尺读数呢?
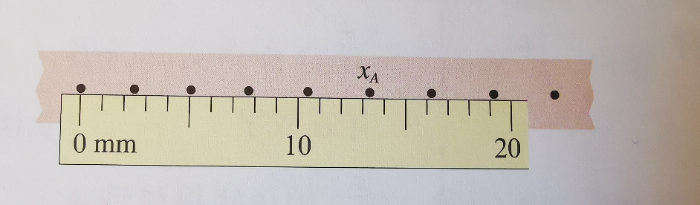
假如我们要读出上图中点A的位置,首先我们一般在读数时,左端0刻度线和起点对齐,然后可以看到A点在13mm到14mm之间,我们使用1mm分度值的尺子要让最后的结果最后一位是估读出的不确定数字,而前面的数字则为精确的数字,也即要读到最小分度值的下一位,因此结果可以读作13.3mm,末尾的3虽然不可靠,但还是有用的,因为它能表示点A在13mm和14mm两条刻度线之间,靠近中点但离13mm刻度线稍近的位置。
这种带有一位不可靠数字的近似数字叫做“有效数字”。例如13.3mm是三位有效数字,改写成1.33cm或者0.0133m仍然是三位有效数字。由此可见小数中最前一位非零数字前面的0是表示小数点的位置的,不是有效数字。为了正确表述有效数字,特别大或者特别小的数字都要用科学计数法,例如月球到地球的平均距离为,钨原子的半径为.

如上图所示,如果仍用这把刻度尺测量另一点B的位置,点B的中心恰好与19mm的刻度线正对,这种情况应该如何处理呢?能不能读成19mm呢?答案是不能,必须记录成19.0mm。原因是我们一般习惯让读出的数字最后一位是估读的,而前面的是精确的,如果你告诉别人19.0mm,那么别人就能确定你前面的19都是精确的,而后面的0是你估读的,甚至还能知道你用的就是1mm分度值的刻度尺第19个刻度线正好对准了B的中心位置。这样你的信息才算传达到位。反之如果你告诉别人19mm,别人会以为9是你估读的,而1才是精确的,那样就乱套了,别人会以为你用的是一个1cm分度值的刻度尺,也就是0-10以及10-20之间的小刻度全部不存在,且B的中心位置非常靠近20那个刻度,这样就传达了错误的信息。由此可见最末一位的数字0是有意义的,不能随便舍去或添加。
二、电流表电压表的读数
我们再来看看电流表电压表是如何读数的,请你先自行填完下面的空后点击“点击显示答案”进行答案检查。
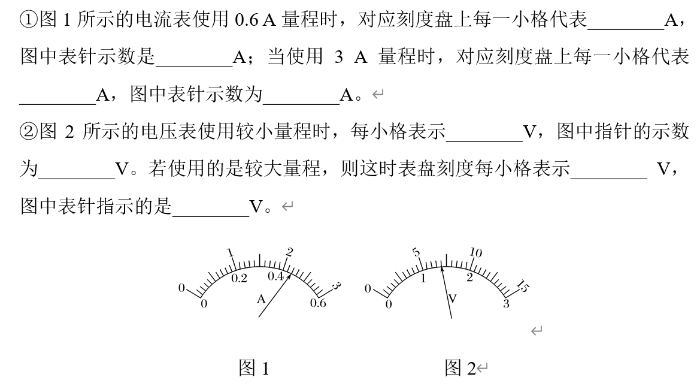
怎么样?做得如何?
我们会发现读电流表和电压表好像又和前面刻度尺的读法不一样了,怎么回事呢?为什么每小格0.02A就不要继续向下一位估读,而是只读到0.01A这一位呢?为什么每小格0.1V的就要向下一位估读,读到0.01V这一位呢?难道是约定俗成,我们前面讲的原则不能用了吗?
其实不然,我们前面讲的原则最后一位是估读数,前面的是精确数仍然是适用的,之所以每小格0.02A不要继续向下一位估读实际上是因为光0.01A这一位都不是确定的,比如指针指在0.44A到0.46A这两个刻度之间时,如果非常接近中间,那么究竟是0.45几A还是0.44几A就是不确定的,那样最后的结果就有了两个不确定数字,因此我们对于每小格是1、0.1、0.01……(末尾是1)的都向下一位估读,而对于每小格末尾不是1的,例如此题中的“0.02A”就不向下一位估读。
三、多用电表的读数
下面我们再来看看多用电表中电流和电压的读数。看看是不是仍然服从我们的原则。请你先自行填完下面的空后点击“点击显示答案”进行答案检查。
如图所示为正在使用中的多用电表表盘,如果是用x100挡测量电阻,则读数为________.
如果是用直流10mA挡测量电流,则读数为______mA.
如果是用直流5V挡测量电压,则读数为________V.
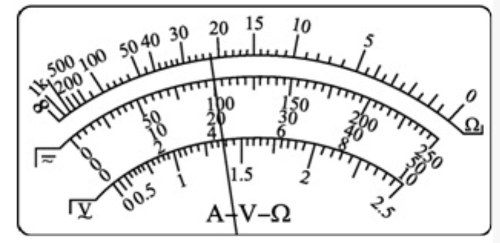
我们可以看到,欧姆表由于刻度不均匀,而我们的肉眼只能在刻度均匀的时候猜出两个刻度之间的读数大概是多少,所以我们的估读是没有意义的,因此欧姆表是个例外,它不估读。
而电流档和电压档全部是符合我们前面所说原则的。
四、电阻箱的读数
下面我们再来看一个比较特别的——电阻箱。
这是2019年全国三卷的电学实验题。

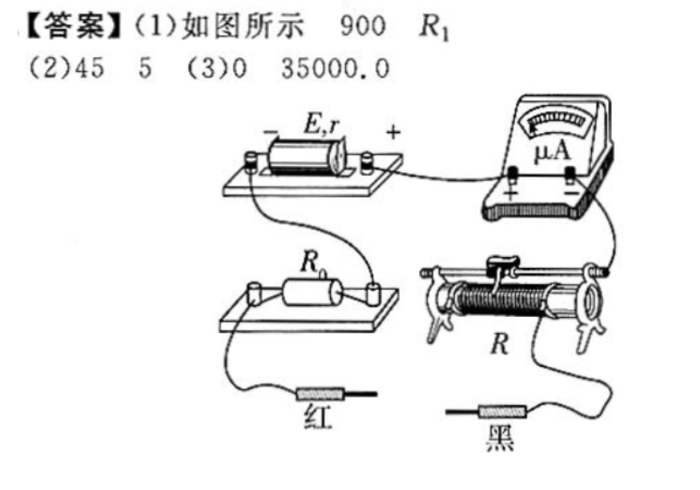
这题就不让大家完整做一遍了,因为不是我们本节的重点,关键是让大家看一看最后的这个电阻箱读数的问题,你会怎么读数呢?35000?35000.00?
以上两种读法都是错误的!必须读成35000.0!为什么呢?只要抓住了读数的原则其实也很好理解,我们读数就是要读出的数据尽量包含丰富的信息,且信息要准确且有意义。为了体现精确度,最后的“.0"当然不能舍去,而我们为什么也不估读呢?显然这里指针都是直接对齐的,读出来多少就是多少,根本没有估读的机会也自然没有估读的必要以及意义,因此这里也自然不估读。
下面是此题的答案,感兴趣的同学可以做一做对一对,在此就不再赘述了。
五、游标卡尺读数
下面我们再来介绍游标卡尺。
下图是游标卡尺的实物图。

下图是游标卡尺的构造示意图。
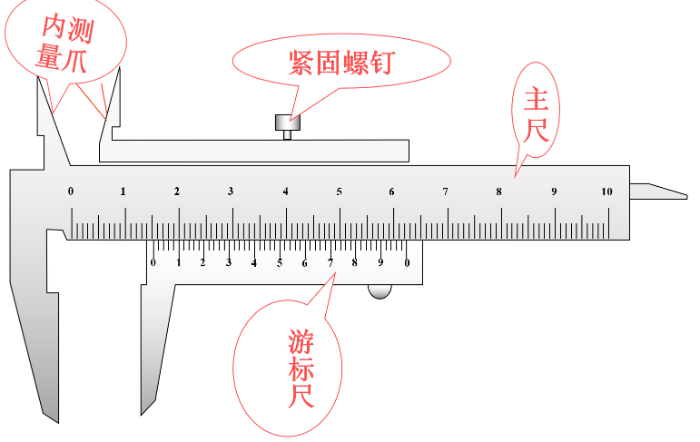
为了帮助你更好地理解游标卡尺的原理,下面是依据其原理制作的,上面较密集的线代表主尺,下面的11条较宽的线则代表游标尺。相邻两个线之间的距离相等。请你首先把下面的滑动条k向左拖动到0,可以观察到下面的游标尺最右边与主尺的倒数第二条线对齐,因此主尺是把10个单位长度分成了10大格,每大格1个单位长度,接着短线又把一个单位长度分成5份,每小格0.2个单位长度。而游标尺则把9.8个单位长度分成10份,每大格0.98个单位长度。
下面我们拖动k滑动条,可以看到随着k的增加,游标尺上的线依次与主尺上的长线对齐,比如在k=0.02时,游标尺上的第二条线与主尺上的第二条长线对齐,又因为根据前一段的分析我们已经知道主尺相邻两个长线的距离是一个单位长度,而游标尺相邻两个长线的距离是0.98个单位长度,因此主尺第一条线和游标尺第一条线之间的距离为0.02个单位长度,即待测物体宽度为0.02.同理,当k=0.04时,游标尺第三条线和主尺第三条长线对齐,游标尺的第一条长线到第三条长线只有0.98*2个单位长度,因此被测物体宽度为0.04个单位长度……我们可以发现当k从0取到0.2时(即待测物体宽度从0到0.2时),游标尺的第一条线从主尺的第一条线每次移动0.02,直到移动到第二条线,就好像把主尺的最小分度0.2给10等分了一样。
通过上面的分析我们一方面发现这种尺子测量物体宽度只能取得0、0.02、0.04、0.06……这些值,因此我们说这种尺子的精度为0.02.而这个0.02如果数学化表达一下就是将主尺的最小分度0.2除以游标尺的格数10即可,即0.2/10=0.02.
这样我们就得到了读数规律:首先读出游标尺第一条线向左对应的主尺上的刻度,接着看游标尺第几条线和主尺对齐,若是第n条线对齐,那么就在原来主尺上刻度的基础上加上(n-1)*(主尺分度值/游标格数)。(PS:这里的第n条线和一般资料书上的第n条线不是一个意思,一般资料书上是把第二条线视为第一条线的)由于真实测量时总是能看到对齐的线,因此不存在估读的机会和必要,自然游标卡尺不估读。
下面我们将这种规律运用到实际的做题中试一试看!
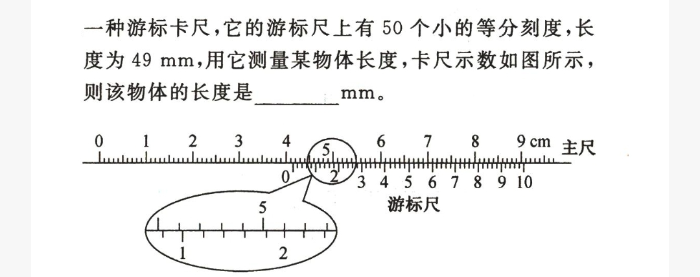
分析:首先看游标尺第一条线左边主尺对应的读数为41mm,接着由于游标尺的第21根线(包含了第一条0刻度线)与主尺对齐,且主尺最小分度为0.1cm,游标格数为50.因此读数为:”主尺上刻度的基础上加上(n-1)*(主尺分度值/游标格数)“=41mm+(21-1)*(0.1cm/50)=41mm+20*0.02mm=41.40mm,末尾的0不能省去,也不能多添加,因为这种尺子的精度就是0.1cm/50=0.02mm。
六、螺旋测微器读数
此为螺旋测微器实物图

此为螺旋测微器构造示意图
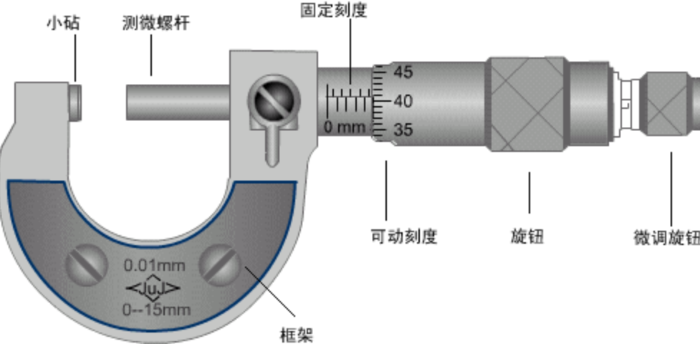
同样地,为了帮助你更好地理解螺旋测微器的原理,下面是依据其原理制作的,请你将可变刻度从0调至0.5,可以观察到随着旋钮的旋转,正好固定刻度移动0.5mm,而可动刻度上有50个小格,与前面所介绍的游标原理类似,这里的精度就是固定刻度的最小分度/50,即0.01mm,而我们又可以观察到可动刻度并不是总是正好与固定刻度对齐的,因此可以进行估读,所以最后读出的数据形如”.mm"例如你若将下面固定刻度滑动条调至1.5,可变刻度滑动条调至0.165,则读数为1.5mm+0.165mm=1.665mm.
下面是一些练习题,请你自主完成后自行对照订正。


参考答案:
CD;C;4.118;9.155;C;B
2.25、6.859;4.118;11、21;2.98cm、6.170cm、1.046cm;0.642mm、10.294mm;10.50、1.732