Système multibase 2-3
Vous pouvez entrer un nombre n dans la case correspondante (entier entre 0 et 511). Vous verrez sa décomposition en base deux écrite horizontalement et sa décomposition en base trois écrite verticalement.
Vous pouvez bouger les points qui composent la ligne brisée orange pour écrire le nombre n dans une base entre la base deux et la base trois. On appelle un tel système multibase.
Cette construction est due à Damien Simon.
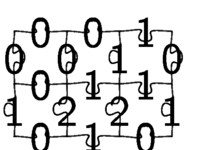
Les six pièces du puzzle
Six pièces de puzzle permettent de passer d'une écriture binaire d'un nombre (à l'horizontal) en son écriture ternaire (en vertical) et vice-versa. Composez d'abord l'écriture binaire (resp. ternaire) d'un nombre horizontalement (resp. verticalement), complétez par des 0 à gauche (resp. en haut), puis résolvez le puzzle vers le haut et à droite (resp. vers la gauche et en bas) pour arriver à une verticale (resp. horizontale) donnant son écriture en base trois (resp. deux).
Si vous prenez par exemple ces six pièces comme départ, vous voyez que vous êtes obligé·e, afin de commencer par des 0 en haut et à gauche, d'obtenir à la fin 1010₂=101₃=8+2=9+1, soit dix.
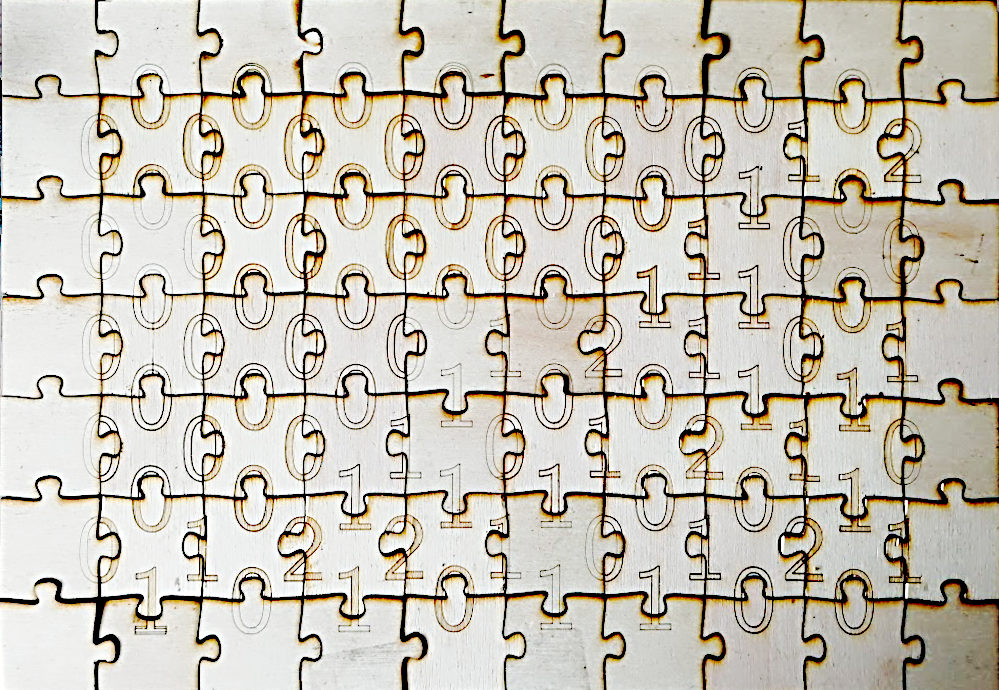
Une version PDF prête à être découpée: vert en écriture, puis rouge en découpe.
Si on n'a pas de découpeuse laser, on peut simplement imprimer sur du carton, colorier les chiffres et découper les carrés. Ici, 333 en base dix s'écrit 101001101₂ et 110100₃.
