SR0 - Geometria descriptiva - Fonaments
LA TEORIA:
La geometria descriptiva és una branca de la matemàtica que té com a objectiu fonamental representar sobre una superfície de dues dimensions, com són un full de paper o una pantalla d'ordinador o mòbil, cossos volumètrics tridimensionals situats a l'espai.
Per fer-ho, es projecte els objectes damunt d'un pla de referència (pla del quadre) i se n'obté la representació bidimensional. Aquesta projecció la podem veure amb la ombra que projecta un llum, el sol, un projector o l'ull humà.
PROJECCIÓ:
Projectar un objecte consisteix a obtenir-ne una representació damunt d'una superfície que es coneix com a pla del quadre o pla de projecció.
En els diversos sistemes de representació, la projecció sobre el pla del quadre es fa mitjançant els raigs o feixos projectants que surten d'un punt anomenat centre de projecció.
Els raigs o feixos projectants són línies imaginàries que, passant pels vèrtexs dels objectes, proporcionen en la seva intersecció amb el pla del quadre la projecció d'aquest vèrtex.
Depenent del centre de projecció, la relació entre els raigs i el pla del quadre i la situació dels cossos geomètrics respecte aquest trobarem els diferents sistemes de representació.
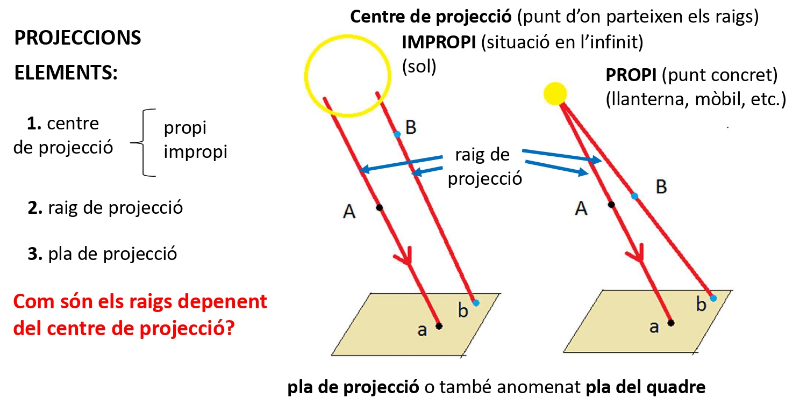
Depenent del centre de projecció, la relació entre els raigs i el pla del quadre i la situació dels cossos geomètrics respecte aquest trobarem els diferents sistemes de representació.
TIPUS DE PROJECCIÓ SEGONS EL CENTRE O ORIGEN DE PROJECCIÓ.
Projecció cilíndrica. L'Origen dels raigs projectants és l'infinit (punt impropi), és a dir, els raig de projecció són paral·lels entre ells. Un exemple serien les ombres a terra de qualsevol objecte que provoca el sol.
- Quan els raigs són ortogonals (perpendiculars) al pla del quadre s'anomena projecció cilíndrica ortogonal.
- Quan els raigs són oblics respecte el pla del quadre s'anomena projecció cilíndrica obliqua.
Pots moure els punts blaus per veure com es modifiquen les projeccions.
Intenta respondre a aquestes preguntes?
- Com són les projeccions dels segments si aquests estan sobre un pla horitzontal?
- Si són horitzontals tenen la mateixa longitud? segueixen sent paral·lels?
- Si no són horitzontals, tenen la mateixa longitud? segueixen sent paral·lels?
- Com són les longituds dels segments A'B' dels dieferents tipus de projecció respecte AB?
- En la projecció cònica, podria ser que la projecció del triangle ABC fos més petita que l'original?
Ara podem veure la projecció però de cares i no arestes, ho podem veure en el següent document.
Modificant el tipus de pla i el tipus de llum podrem veure els diferents sistemes projectius.
El mateix document per veure amb ulleres 3D.
SISTEMES DE REPRESENTACIÓ
Els sistemes de representació són els diferents mètodes que s'utilitzen en dibuix tècnic per representar els cossos geomètrics (3D) sobre una superfície (2D) com pot ser un paper, una pissarra, un vidre, una fotografia, un ordinador, un mòbil, etc...
Existeixen quatre sistemes principals de representació, dels quals també hi ha diferents variants: el sistema acotat, el sistema dièdric, el sistema axonomètric i el sistema cònic.
La representació dependrà del tipus de projecció, de la situació del pla del quadre i la relació d'aquest amb el cos geomètric. Segons el tipus de projecció que s'obté permetrà uns tipus de funcions o unes altres.
Sistemes de mesura. Permeten prendre mesures directament sobre el dibuix per obtenir d'una manera ràpida les dimensions i la posició dels objectes. Els sistemes de mesura són el sistema acotat i el sistema dièdric. L'inconvenient és que no es poden apreciar només amb un cop d'ull la forma i les proporcions dels objectes representats, es requereixen uns coneixements previs per poder entendre els cossos representats.
Sistemes representatius. Mostren els objectes mitjançant una única projecció, en el qual, només amb un cop d'ull, es poden apreciar la forma i les proporcions d'aquests objectes d'una manera similar a com els observem a la vida real. Els sistemes que es consideren representatius són el sistema axonomètric i el sistema cònic. Tenen l'inconvenient que són més laboriosos i difícils de fer.