GM2 PEI-2 2023
Enunciado
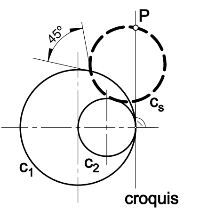
Determinar la circunferencia cs, indicada en el croquis, que forma 45º con c1, es tangente a c2 y pasa por el punto P.
Resolución
Dado que se tiene un punto de paso en el eje radical de las circunferencias c1 y c2 lo más sencillo es
1- Realizar una inversión de centro I=P.
2- Al tener I la misma potencia con respecto a c1 y c2 la potencia de inversión que hace que c1=c'1 y también hace que c2=c'2. En el plano inverso la solución buscada será una recta s', tangente a c'2 y que forma 45º con c'1.
3- Las rectas que forman 45º con c'1 son tangentes a la goniómetra de 45º (g45º) de c'1. Para determinar dicha goniómetra se traza una recta cualquiera que forme 45º con c'1. Dado que las circunferencias tienen líneas de centros es trivial determinar dicha recta.
4- La goniómetra g45º es tangente a la recta y concéntrica con c'1, con lo que su radio R se puede determinar con una perpendicular.
5- La recta s' será tangente a c'2 y a g45º. Para calcularla se puede, por ejemplo, determinar el centro de homotecia H+ que relaciona ambas circunferencias, haciendo uso de dos puntos homotéticos E y EH.
6- Haciendo uso de un arco capaz de 90º entre H+ y el centro de c'2,
7- se determina el punto de tangencia T' sobre c'2, y por lo tanto s'.
8- Es necesario invertir para obtener la solución en el plano original. Para ello nos podemos olvidar de la goniómetra (nótese que al no ser una circunferencia que pertenezca al haz definido por c1 y c2 la goniómetra g45º no se invierte en ella misma, y por lo tanto la solución cs no será tangente a ) y de las construcciones necesarias para obtener s'. La perpendiculara s' por I es un lugar geométrico de Os, centro de cs.
9- Como T' pertenece a c'2, se puede determinar fácilmente su inverso, T, punto de tangencia entre cs y c2.
10- El radio de c2 por T, es otro lugar geométrico del centro de la solución.
11- Con lo que quedan definidas Os y cs. Como se puede comprobar, cs y c1 forman 45º.
12- También se puede comprobar que los puntos A' y B', intersección entre c'1 y s'. se invierten en los puntos A y B, intersección entre c1 y cs.
13- Aquí se puede ver la solución y su inversa, sin apenas trazados auxiliares. Nótese que tanto el punto P como el centro de c2 se pueden mover para modificar el enunciado del problema.