Moto parabolico
Studio del moto parabolico con Geogebra
In geometria analitica, abbiamo studiato una particolare conica: la parabola.
Abbiamo visto che, quando in particolare l'asse di simmetria della parabola è parallelo al'asse y, la sua equazione è del tipo:
Utilizza l'applet Geogebra sottostante per ripassare il significato geometrico dei parametri a, b e c dell'equazione della parabola:
Equazione della parabola
Qual è il significato geometrico dei parametri a,b,c?
Asse di simmetria della parabola
L'equazione dell'asse di simmetria della parabola è:
Il moto di caduta di una biglia
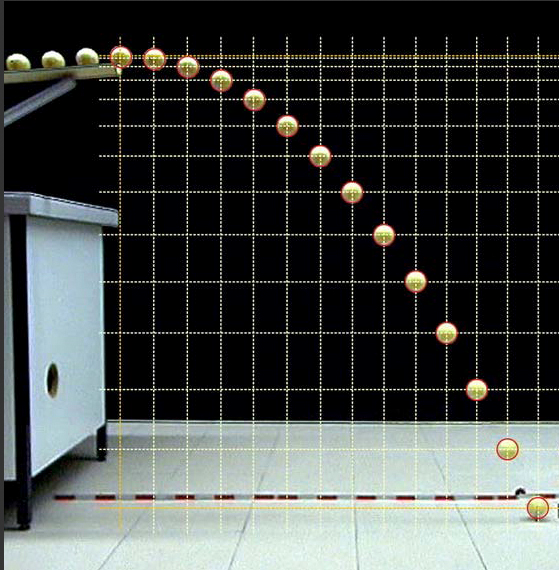
Modifica i parametri a,b e c della parabola per ottenere una curva in grado di approssimare il moto della biglia
Sei riuscito a soddisfare la richiesta? Se si, scrivi i valori dei parametri a, b, c che hai ottenuto.
Considera ora questa nuova situazione. Inserisci l'equazione parametrica della parabola e prova a riprodurre uno qualunque dei getti della fontana. Discuti i risultati che ottieni.
Inserisci in questo spazio le tue considerazioni:
Il moto orizzontale e il moto verticale
Riprendiamo in esame il moto della biglia che lascia il piano. La griglia fissa la posizione della biglia con cadenza data dall'intervallo temporale tra i frame. Osservane la spaziatura orizzontale e verticale. Separando idealmente il moto verticale da quello orizzontale cosa si può dire di questi due moti?
Equazioni parametriche del moto
Consideriamo le equazioni:
Sei in grado da qui di ricostruire l'equazione della parabola?