Geogebra HW#1
- Author:
- jasoncros
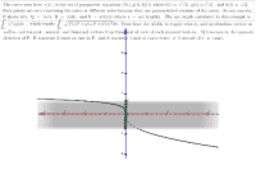
The curve seen here, r(t), is the set of parametric equations (f(t), g(t), h(t)) where f(t) = 2t, g(t) = sin(t), and h(t) = e^t. Four points are seen traversing the curve at different rates because they are parametrized versions of the curve. As one can see, P shows r(t), Q = r(-t), R = r(3t), and S = r(t(s)) (where s = arc length). The arc length calculated in this example is the integral of the speed of the curve from reference point, 0, to t [math][/mathf(x)=2](where t ranges from -5 to 5). Users have the ability to toggle velocity and acceleration vectors, as well as unit tangent, normal, and binormal vectors from the point of view of each parametrization.