Finding the Median of a Trapezoid
Analyze the dimensions of the trapezoid around and use the slider to create a parallelogram.
Use the slider to transform the trapezoid into a parallelogram. Observe the different dimensions/measurements of the parallelogram and the trapezoid and compare their shapes and properties. Which of the following properties do trapezoids possess that are different from parallelograms?
Use the slider to transform the trapezoid into a parallelogram. Base 1 has a length of 12 inches, Base 2 has a length of 4 inches, and the height of the trapezoid is 7 inches. Use your knowledge of calculating the area of a parallelogram to calculate the area of the trapezoid. What is the area of the trapezoid?
Area of Trapezoid
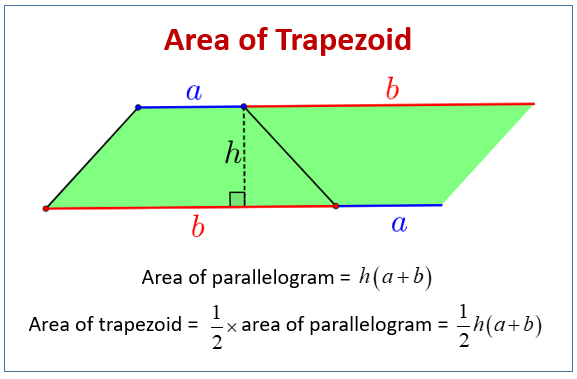
Analyze this trapezoid without sliding the red line. In this instance, c is Base 1 and a is Base 2. Using what you now know about the formula for calculating the areas of trapezoids and parallelograms, hypothesize the formula used to find the midpoint (also know as the median) of this trapezoid.
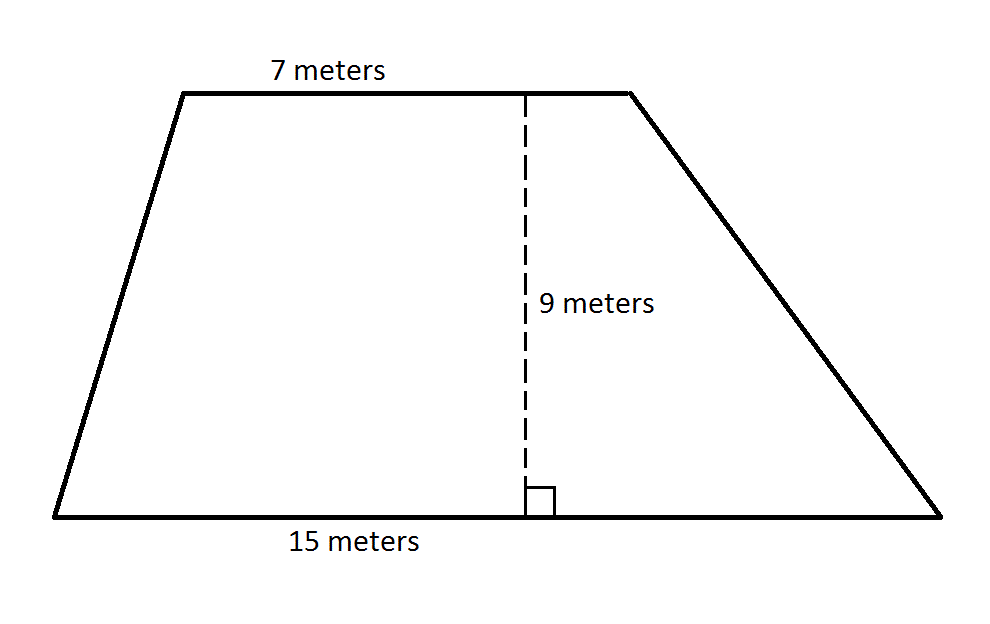
Observe this trapezoid. Now with the knowledge of calculating trapezoid medians, calculate the median for this specific trapezoid given the allotted dimensions and measurements.