GeoGebra

Grenzwerte für x gegen unendlich

Autor:Caroline Ryser

Übung 1

Überprüfe, ob alle folgenden Funktionen den Grenzwert 0 haben:
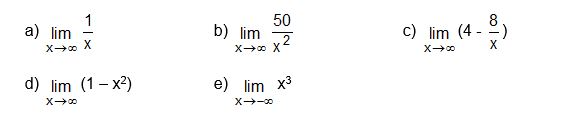
Image

Übung 2

Zeichne den Grafen von f(x) = 2x.
  1. Bestimme den Grenzwert für x und für x .
  2. Was ändert sich, wenn f(x) = 2-x ist?

Übung 3

Berechne jeweils den Grenzwert folgender Betragsfunktionen (zur Erinnerung: Den (absoluten) Betrag einer reellen Zahl erhält man durch Weglassen des Vorzeichens. Auf der Zahlengeraden bedeutet der Betrag den Abstand der gegebenen Zahl von Null.):
[size=50]Lösungen: a) 0 b) 0 c) -1[/size]
Lösungen: a) 0 b) 0 c) -1

Übung 4

Bestimme folgende Grenzwerte durch geeignete Berechnungen:
[size=50]Lösungen: a) –1    b) 2/5   c) 0       d) ½[/size]
Lösungen: a) –1    b) 2/5   c) 0       d) ½

Übung 5

Bestimme folgende Grenzwerte durch geeignete "Umformungen":
[size=50]Lösungen: a) 1/3   b) 0      c) -1      d) 1 [/size]
Lösungen: a) 1/3   b) 0      c) -1      d) 1

Übung 6

Knacknüsse!
[size=50]Lösungen: a) 2/3   b) 0      c) 1/3    d) [math]\sqrt{2}[/math]  e) 0      f) 0       g) [math]\infty[/math]      h) 1[/size]
Lösungen: a) 2/3   b) 0      c) 1/3    d)   e) 0      f) 0       g)       h) 1

Übung 7

Suche Funktionen, die für x folgende Grenzwerte haben:
  • 0
  • 1
  • -4
  • 8
  • -
  • keinen

Neue Materialien

Entdecke Materialien

Entdecke weitere Themen