polynomial with complex coefficients
The fundamental theorem of algebra - a visual proof
http://weitz.de/fund/
Der Fundamentalsatz der Algebra (anschaulicher Beweis) Do not set ai=0, use checkboxes to switch on/off using coefficient ai.
The function f(x) CAS (1) has probably to be set manually if cell do not actualize - mark cell + Num Eval.
Hints:
ai complex coefficient of p(z) - input of values
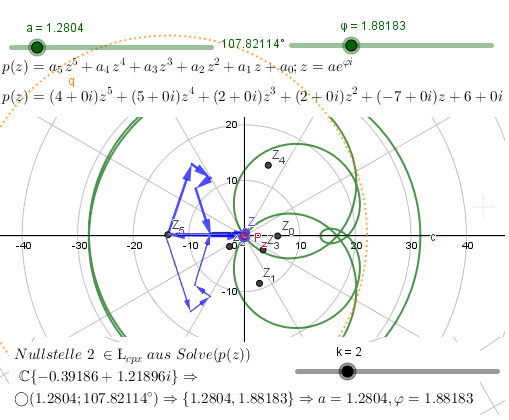
polarcoordinates (mi; ωI)
z=(a ; φ) polarcoordinates - sliders on top - (0<=a<=10)
Zi = ai zi polynom summand in polarcoordinates =( mi ai ; ωi + i φ) -> vectors vi
c(t) parametric curve of polynom p(z) - graph p(z)
Pz = p(z)
App - Darstellung der 3. Nullstelle p(z): :
Do not set ai=0, use checkboxes to switch on/off using coefficient ai.
The function f(x) CAS (1) has probably to be set manually if cell do not actualize - mark cell + Num Eval.
Hints:
ai complex coefficient of p(z) - input of values
polarcoordinates (mi; ωI)
z=(a ; φ) polarcoordinates - sliders on top - (0<=a<=10)
Zi = ai zi polynom summand in polarcoordinates =( mi ai ; ωi + i φ) -> vectors vi
c(t) parametric curve of polynom p(z) - graph p(z)
Pz = p(z)
App - Darstellung der 3. Nullstelle p(z): :
 Do not set ai=0, use checkboxes to switch on/off using coefficient ai.
The function f(x) CAS (1) has probably to be set manually if cell do not actualize - mark cell + Num Eval.
Hints:
ai complex coefficient of p(z) - input of values
polarcoordinates (mi; ωI)
z=(a ; φ) polarcoordinates - sliders on top - (0<=a<=10)
Zi = ai zi polynom summand in polarcoordinates =( mi ai ; ωi + i φ) -> vectors vi
c(t) parametric curve of polynom p(z) - graph p(z)
Pz = p(z)
App - Darstellung der 3. Nullstelle p(z): :
Do not set ai=0, use checkboxes to switch on/off using coefficient ai.
The function f(x) CAS (1) has probably to be set manually if cell do not actualize - mark cell + Num Eval.
Hints:
ai complex coefficient of p(z) - input of values
polarcoordinates (mi; ωI)
z=(a ; φ) polarcoordinates - sliders on top - (0<=a<=10)
Zi = ai zi polynom summand in polarcoordinates =( mi ai ; ωi + i φ) -> vectors vi
c(t) parametric curve of polynom p(z) - graph p(z)
Pz = p(z)
App - Darstellung der 3. Nullstelle p(z): :polynomial with complex coefficients fkt
Find roots p(z) - z=ae^(φi)
The summands of the polynomial build a vector chain (blue). A root can be found if the vector chain of the coefficients is closed - returning to the origin.

- increase modulus (slider a) so far to have a complete free circular disc around the point of origin Z
- decrease modulus to intersect graph p(z) and origin Z=(0,0) - close vector chain
- zoom graph to position Pz (slider φ) as close as possible to the origin
- (a ; φ ) root in polarcoordinates ==> cartesian coordinates
- check calculated roots in Lcpx - next intersection
3D Visualisation p(z)=g(x,y) Surface (open view 3D Graphics in app)
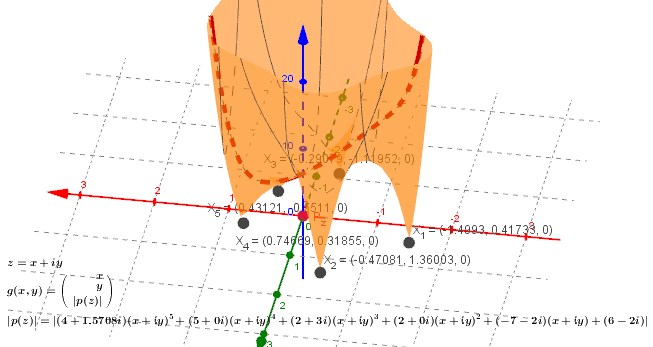
double root (real part ± imaginary part) - multiple point or repeated root