Beschreiben von Funktionsgraphen
Besondere Punkte
Zum einen haben Funktionsgraphen besondere Punkte:
- Nullstellen
- den Schnittpunkt mit der Ordinate
- Extremstellen
- Wendestellen
- Sattelpunkte
Intervall-Arten
Um einen Funktionsgraphen nachvollziehbar zu beschreiben, muss man oft Intervalle angeben.
Intervalle sind Zahlenbereiche auf der Abszisse (x-Achse). Dabei unterscheidet man unterschiedliche Typen von Intervallen:
- Geschlossene Intervalle: (die eckigen Klammern zeigen nach innen) In einem geschlossenen Intervall gehören auch die beiden Randpunkte und dazu. Ein Beispiel: Das Intervall enthält alle Zahlen zwischen und und diese beiden Zahlen selbst.
- Offene Intervalle: (die eckigen Klammern zeigen nach außen), manchmal auch mit runden Klammern geschrieben: Ein Beispiel: Das Intervall enthält alle Zahlen zwischen und , aber diese beiden Zahlen selbst gehören nicht mit dazu.
- Halboffene Intervalle: oder (hier zeigt jeweils eine Klammer nach außen), manchmal auch mit runden Klammern geschrieben: oder Beispiele: Das Intervall enthält alle Zahlen zwischen und , es enthält auch die , aber die gehört nicht dazu. Das Intervall enthält alle Zahlen zwischen und , es enthält auch die , aber die gehört nicht dazu.
Eigenschaften eines Funktionsgraphen, innerhalb eines Intervalls
Folgende Eigenschaften kann ein Funktionsgraph innerhalb eines Intervalls aufweisen:
Steigungen
- Streng monoton steigend, d.h. der Funktionsgraph hat im gesamten Intervall nur positive Steigungen. Ist der Funktionsgraph einer Funktion in einem Intervall streng monoton steigend, dann gilt für alle Zahlen in diesem Intervall: .
- Monoton steigend, d.h. der Funktionsgraph hat im gesamten Intervall nur positive Steigungen und an einzelnen Stellen eine Steigung von Null. Ist der Funktionsgraph einer Funktion in einem Intervall monoton steigend, dann gilt für alle Zahlen in diesem Intervall: .
- Streng monoton fallend, d.h. der Funktionsgraph hat im gesamten Intervall nur negative Steigungen. Ist der Funktionsgraph einer Funktion in einem Intervall streng monoton fallend, dann gilt für alle Zahlen in diesem Intervall: .
- Monoton fallend, d.h. der Funktionsgraph hat im gesamten Intervall nur negative Steigungen und an einzelnen Stellen eine Steigung von Null. Ist der Funktionsgraph einer Funktion in einem Intervall monoton fallend, dann gilt für alle Zahlen in diesem Intervall: .
- Rechts- und Linkskrümmung: Bei Krümmungen betrachtet man eine Funktion immer von kleinen x zu großen x, d.h. von links nach rechts. Wenn der Funktionsgraph in dieser Richtung nach rechts gekrümmt ist spricht man von einer Rechtskrümmung, wenn er nach links gekrümmt ist, ist es eine Linkskrümmung. Krümmungen erkennt man auch an den Funktionswerten der zweiten Ableitung:
- In einem Intervall, in dem die Funktion eine Rechtskrümmung aufweist, gilt für alle x:
- In einem Intervall, in dem die Funktion eine Linkskrümmung aufweist, gilt für alle x:
Lineare, progressive und degressive Steigungen
In der Wirtschaft verwendet man selten die Begriffe Krümmung, sondern man spricht von progressivem oder degressivem Steigen oder Fallen eines Funktionsgraphen:
Bei einer linearen Funktion ist der Funktionsgraph eine ungekrümmte Linie.
- Wenn eine lineare Funktion eine positive Steigung hat, dann sagt man, sie steigt linear.
- Wenn eine lineare Funktion eine negative Steigung hat, dann sagt man, sie fällt linear.
- Wenn ein Funktionsgraph schneller steigt, als eine lineare Funktion, dann steigt der Funktionsgraph progressiv.
- Wenn ein Funktionsgraph langsamer steigt, als eine lineare Funktion, dann steigt der Funktionsgraph degressiv.
- Wenn ein Funktionsgraph schneller fällt, als eine lineare Funktion, dann fällt der Funktionsgraph progressiv.
- Wenn ein Funktionsgraph langsamer fällt, als eine lineare Funktion, dann fällt der Funktionsgraph degressiv.
- Wenn ein Funktionsgraph in einem Intervall progressiv steigt, dann gilt dort für alle x: und
- Wenn ein Funktionsgraph in einem Intervall degressiv steigt, dann gilt dort für alle x: und
- Wenn ein Funktionsgraph in einem Intervall progressiv fällt, dann gilt dort für alle x: und
- Wenn ein Funktionsgraph in einem Intervall degressiv fällt, dann gilt dort für alle x: und
Ein Beispiel:
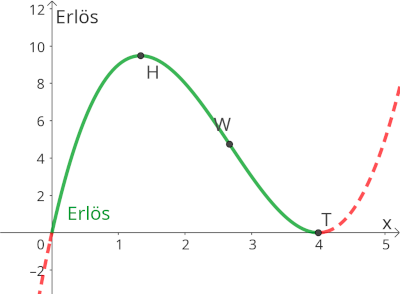
Beschreibung der oben abgebildeten Erlösfunktion
Der Funktionsgraph der Erlösfunktion beginnt im Nullpunkt, hat einen Hochpunkt etwa an der Stelle , einen Wendepunkt bei ungefähr und die Sättigungsmenge ist eine doppelte Nullstelle bei , weil der Funktionsgraph die Abszisse hier nur berührt (Mehrfache Nullstellen siehe hier).
- Der Funktionsgraph steigt von bis zum Hochpunkt H degressiv.
- Zwischen dem Hochpunkt H und dem Wendepunkt W fällt der Funktionsgraph progressiv
- Zwischen dem Wendepunkt W und der Sättigungsmenge beim Tiefpunkt T fällt der Funktionsgraph degressiv.
- Das Intervall rechts vom Tiefpunkt T gehört zwar nicht mehr zum ökonomisch sinnvollen Definitionsbereich, dies ist aber ein Beispiel für eine progressive Steigung
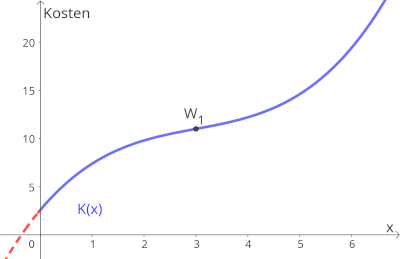
Beschreibung der oben abgebildeten Kostenfunktion
Der Funktionsgraph ist über den gesamten Definitionsbereich streng monoton steigend. Die Fixkosten sind bei etwa 2,5 GE und der Funktionsgraph hat einen Wendepunkt bei x=3 ME.
- Die Kostenfunktion steigt degressiv von bis zum Wendepunkt W.
- Die Kostenfunktion steigt rechts vom Wendepunkt W progressiv.
Aufgabe
Sehen Sie sich auf der Seite "Monopol und Polypol" die Funktionsgraphen der Preis-Absatzfunktion, der Erlösfunktion, der Kostenfunktion und der Gewinnfunktion an und beschreiben Sie die Funktionsgraphen mit allen besonderen Punkten sowie den Steigungen im jeweils sinnvollen Definitionsbereich.