Números Complexos 01
No vídeo os números complexos são apresentados, através de uma analogia sobre dualidade. O que podemos dizer que representa essa dualidade nos números complexos?
- A
- B
- C
- D
- E
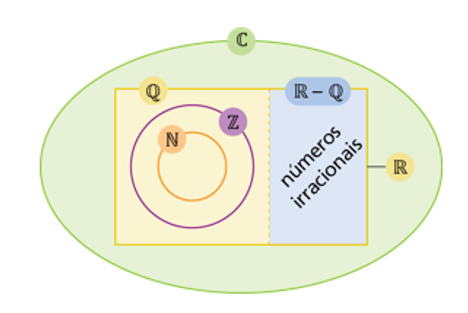
Com relação ao diagrama acima, assinale o item verdadeiro.
- A
- B
- C
- D
- E
Assinale o item que apresenta as raízes da equação x2 + 1 = 0
- A
- B
- C
- D
- E
Com relação as partes real e imaginária do número complexo a seguir, assinale o item correto.
- A
- B
- C
- D
- E
Assinale o item que apresenta um número complexo imaginário puro.
- A
- B
- C
- D
- E
Sabendo que os números complexos z e w, apresentados a seguir, são iguais, qual o valor x.y?
- A
- B
- C
- D
- E
Obs.: faça a resolução no caderno e coloque a foto no bloco de notas correspóndente.Qual o valor de z + w?
Qual o valor de z - w?
Qual o valor de 3z - 2w?
Qual o valor de z.w?
Qual o conjugado do número complexo z?
- A
- B
- C
- D
- E
Efetue no seu caderno, a divisaão a seguir e bata a foto da resolução e mostre aqui.
Qual o valor da potência abaixo?
- A
- B
- C
- D
- E
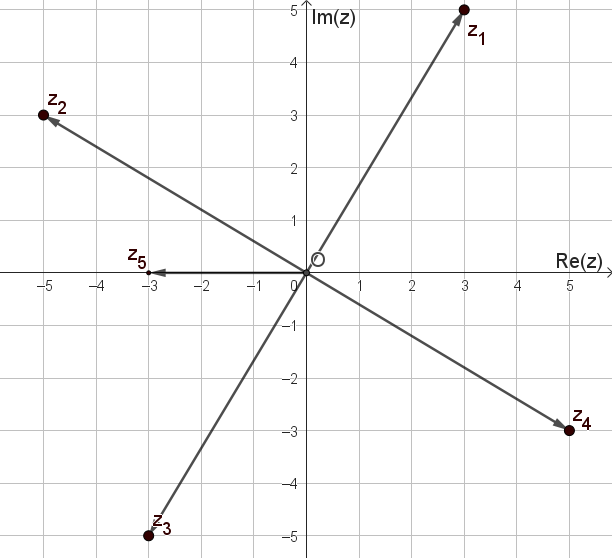
Qual é o número complexo, resultado da soma acima?
- A
- B
- C
- D
- E
Observando a figura a seguir, assinale o item verdadeiro, com relação ao módulo e argumento de um número complexo.
- A
- B
- C
- D
- E
Localizado o número complexo corretamente, responda aqui qual o módulo |z1| (Use o Teorema de Pitágoras) e o argumento ,de z1.