Google ClassroomGoogle Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Activity 4 - Concreção 8215

ForfatterCláudia Oliveira de Almeida Santos

Figure 6 - Concreção 8215

Figure 6 - Concreção 8215
Concreção 8215, 1982 Tempera on canvas 80 cm x 80 cm L. Biezus Collection Source: Sacilotto, 2021
In this activity, we will reinterpret the artwork Concreção 8215 using the Sequence command in GeoGebraScript. First Steps
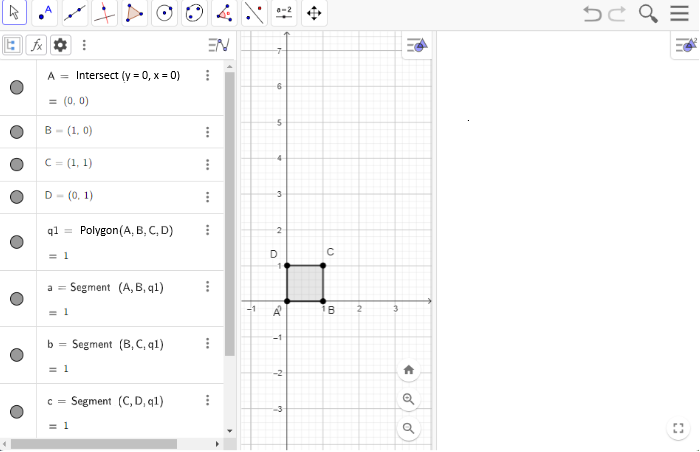
  1. First, we will create a square q1 with vertices at the points A(0,0), B(1,0), C(1,1), and D(0,1). To keep the construction clear and uncluttered, remove the labels from the segments and the polygon if they are visible.
  2. It is recommended to open a second viewing window so that the geometric construction of the reinterpretation does not overlap with the final result.
Source: The Author.
Source: The Author.

Identifying Shapes and Geometric Properties in Concreção 8215

Observe that Concreção 8215 is a composition formed by rotated and translated squares, arranged in rows and columns, resulting in a larger square composed of multiple smaller units.

Question 1

How many squares are arranged in the rows and columns of this composition?

Tjek dit svar

Question 2

What is the rotation angle applied to transform one square into the next in sequence in the first row?

Tjek dit svar

Creating a Sequence of Points

To create a sequence of points using GeoGebraScript, we will use the Sequence command in the following form: Sequence(Expression, Variable, Initial Value, Final Value). With this command, we can generate either a row of squares or a grid containing multiple squares arranged in rows and columns, as seen in this artwork. This allows for an efficient replication of the geometric pattern present in the composition.
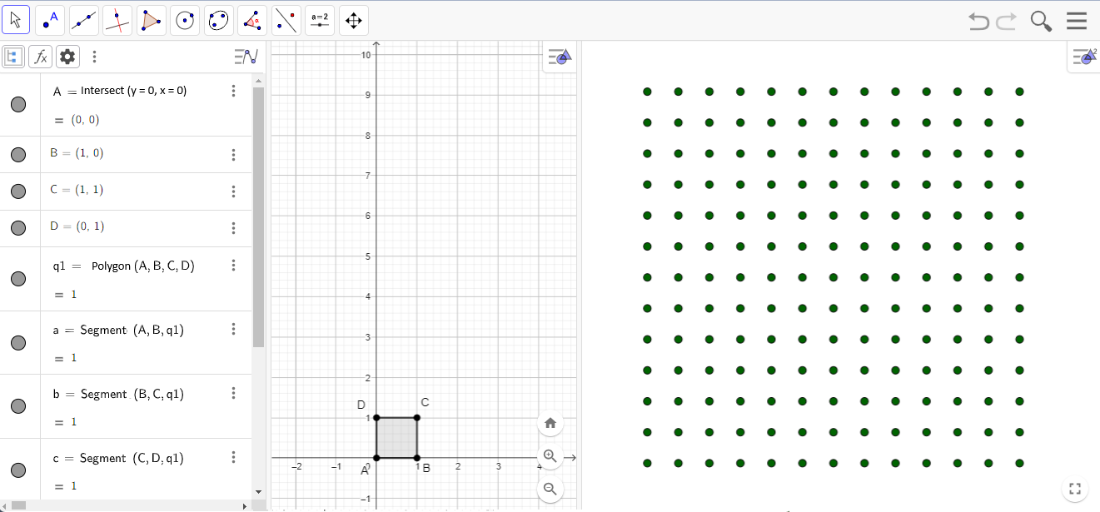
  1. We will create a set of points arranged in 13 rows by 13 columns. To do this, we define n = 13 as the number of points to be created per row and column.
  2. After entering n = 13 in the Algebra menu, a natural number slider is automatically created, highlighting n = 13. This allows the value of n to be adjusted according to the configuration set for the slider.
  3. To create the 132 points, we need to specify their coordinates, providing both their x-coordinate (abscissa) and y-coordinate (ordinate). To achieve this, we use the Sequence command:
L = Sequence((Mod(i,n),Division(i,n)),i,0,n²-1)

Question 3

Identify the expression, the variable, the initial value, and the final value in this command.

Tjek dit svar

Question 4

Considering that n = 13, what values will the variable i take in this sequence?

Tjek dit svar

Question 5

What does the expression (Mod(i, n), Division(i, n)) mean in the Sequence command, considering that i represents the variable?

Tjek dit svar
After the sequence of points is created, you should be able to visualize the ordered pairs as shown in the following image.
Image

Creating a sequence of squares.

We will use the created points as the centers of squares that result from translations and rotations of the square q1, considering E as the center of this square. To do this, we can use the Sequence command as follows: M = Sequence(Translate(Dilate(Rotate(q1, (x(L(i))+y(L(i)))(-15°), E), 0.5, E), L(i)), i, 1, n²)*

Question 6

Identify the expression, the variable, the initial value, and the final value in the command M = Sequence(Translate(Dilate(Rotate(q1, (x(L(i))+y(L(i)))(-15°), E), 0.5, E), L(i)), i, 1, n²)

Tjek dit svar

Question 7

In the expression (Translate(Dilate(Rotate(q1, (x(L(i)) + y(L(i))) * (-15°), E), 0.5, E), L(i))), what does the command (Rotate(q1, (x(L(i)) + y(L(i))) * (-15°), E)) represent?

Tjek dit svar

Question 8

In the expression (Translate(Dilate(Rotate(q1, (x(L(i)) + y(L(i))) * (-15°), E), 0.5, E), L(i))), what does the command (Dilate(Rotate(q1, (x(L(i)) + y(L(i))) * (-15°), E), 0.5, E) represent?

Tjek dit svar

Question 9

Explain the expression (Translate(Dilate(Rotate(q1, (x(L(i)) + y(L(i))) * (-15°), E), 0.5, E) considering the commands explained in the previous questions.

Tjek dit svar

Question 10

Return to the construction started in GeoGebra online and, in the Input field of the Algebra menu, enter the command: M = Sequence(Translate(Homothety(Rotate(q1, (x(L(i)) + y(L(i))) * (-15°), E), 0.5, E), L(i)), i, 1, n²). If necessary, configure M to be displayed in View 2. Compare the reinterpreted version created through the sequence with the representative image of Concreção 8215. In your opinion, does the reinterpretation remain faithful to the original artwork? Justify your answer, considering geometric and symmetrical aspects as well as the arrangement of the shapes in the composition.

Tjek dit svar
Next, we present an interactive activity developed using the commands discussed throughout this task. Explore it by clicking the available buttons, following the sequence of object creation. Step 1: Start by generating translations, rotations, and homotheties of the original polygon. Step 2: Create a reinterpretation of the artwork Concreção 8215. We invite you to interact with the activity, creating your own reinterpretations, including variations in the shape of the original polygon to explore new compositions.

Nye Materialer

Opdag Ressourcer

Udforsk emner