Atividade IV.I: Mediatrizes e Circuncentro - Material Virtual
- A Mediatriz de um triângulo é uma reta que passa pelo ponto médio de um lado do triângulo e é perpendicular a esse lado;
- O Circuncentro de um triângulo é o ponto de intersecção das mediatrizes de um triângulo, ou seja, o ponto onde as três mediatrizes se encontram.
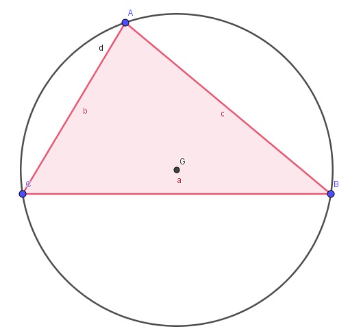
Passo a passo para a construção das mediatrizes e circuncentro de um triângulo.
Passo 1: no triângulo abaixo, destaque os pontos médios dos lados do triângulo com a ferramenta da janela 2;
Passo 2: use a ferramenta da janela 3, para traçar retas perpendiculares passando pelos pontos médios, (lembre-se o ângulo de 90° precisa ser com o lado do triângulo);
Passo 3: Destaque o ponto de intersecção entre as retas utilizando a ferramenta da janela 4.
Responda:
1. Movimente o triângulo. O ponto de intersecção entre as mediatrizes é sempre interno ao triângulo?
2. Por que o circuncentro está sempre equidistante dos vértices do triângulo? Como isso pode ser útil na prática?
No applet abaixo:
Passo 1: esconda as retas perpendiculares e os pontos médios do triângulo utilizando a
ferramenta;
Passo 2: Construa uma circunferência, utilizando a janela 6, dados o centro (ponto G) e um dos vértices do triângulo.
Responda:
3. Por que o circuncentro é equidistante de todos os vértices do triângulo?
4. Como a localização do circuncentro varia com o tipo de triângulo (acutângulo, retângulo, obtusângulo)?
5. O que ocorre com o raio da circunferência circunscrita ao modificarmos o tamanho do triângulo?
6. Se você fosse projetar um objeto com três pontos de contato, como uma mesa triangular, onde colocaria o ponto de suporte? O circuncentro seria uma boa escolha?