Second Kepler's law: The law of equal areas
Planets sweep out equal areas in equal time.
The geometric proof of the second Kepler's law presented by R. Feynman corresponded to the proof which was published by Isaac Newton in his Principia (Philosophiæ Naturalis Principia Mathematica / Mathematical Principles of Natural Philosophy, 1697).
Feynman used almost an identical illustration to the original one by Newton:
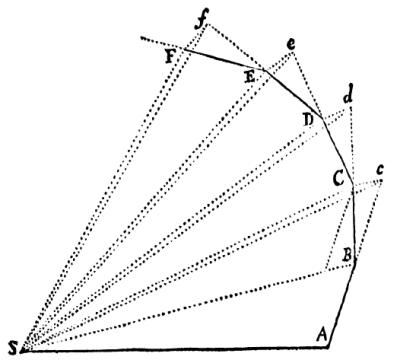
Illustration from: Newton's Principia: the mathematical principles of natural philosophy by Sir Isaac Newton; translated into English by Andrew Motte, New-York: Published by Daniel Adee, 1846.
This geometric proof is based on the elementary properties of a triangle, particularly on the way of the computation of its area.
Exercise: Given triangles SAB, SAC, SBC and SBD (D is movable along p) in the figure below so that B is the midpoint of the segment AC and p is parallel to SB. Determine the relations of areas of all the given triangles. Justify your claim.
Exercise: See the figure below. Points A, B, C,D and E are the successive positions of a planet in its orbit around the Sun (point S) at equal intervals of time. Then, due to the law of inertia |AB| = |Bc|, |BC| = |Cd| and |CD| = |De|.
In accordance with statement of the 2nd Kepler's law (the law of equal areas) it follows that the areas of triangles SAB, SBC, SCD and SDE are equal. Prove it. You can do it gradually, using triangles SBc, SCd and SDe (be aware that cC, dD and eE are parallel to BS, CS and DS, respectively).
The 2nd Kepler’s law (the law of equal areas) appeared to be a consequence of the law of inertia (Newton’s first law) and the fact that changes in motion of planets are caused by the gravitational force directed toward the Sun.
What causes the elliptical shape of a planet's orbit?