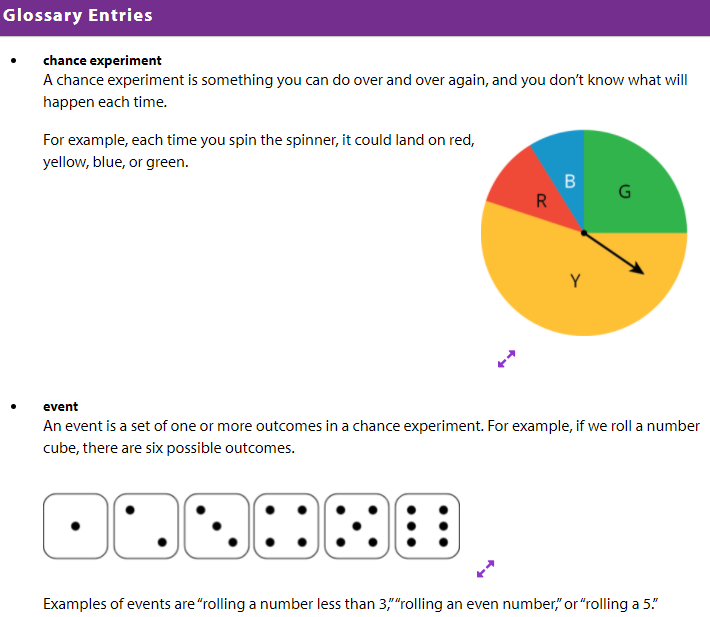
L8.1 - Up to Chance
Learning Intentions and Success Criteria
- Compare probability models and observed frequencies
- Determine whether a given situation involving probability is a chance experiment
- Find or estimate probability using a model or data from a chance experiment
- Identify chance experiments
1.1: Which One Doesn’t Belong: Spinners
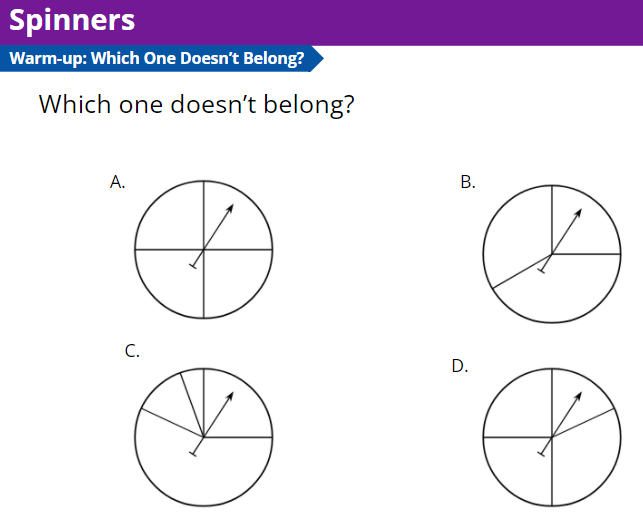
Which one doesn't belong?
1.2: You’re Saying There’s a Chance?

1. Based on the description, rank the quizzes in order from worst expected grade to best.
2. For each of the 3 quizzes, explain why you think chance played a large or small role in determining Elena’s score.
3. For the second and third quizzes, Elena did not look at the questions. Explain why you think she might do better on one than the other.
4. What percentage of the questions do you think Elena will get right on each quiz? Explain your reasoning.
5. For the second quiz, the teacher made a mistake and each of the questions had two correct answers. The teacher accepted either of the correct answers for full credit. What percentage of the questions do you think Elena will get right on the second quiz with the new scoring? Explain your reasoning.
1.3: A Fair Game
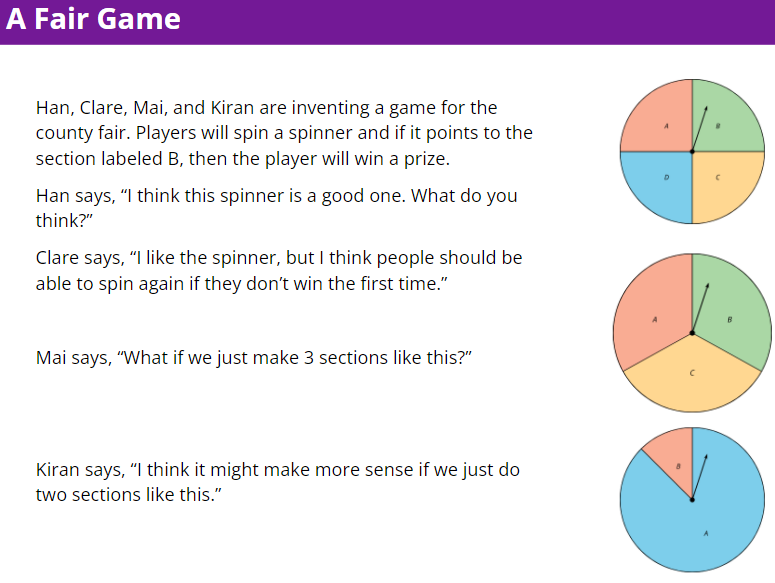
1. Put the proposals in order of the probability that a player will win using that method from least to greatest. Explain your reasoning. Share your explanation with a partner.
2. Each student writes a computer program to play the game using the method they suggested. The computer runs the program for a short time and reports the number of wins and losses. Use the results to estimate the probability of winning using each method.
3. By talking to their friends, they figure out that a good probability for winning is about since it will let enough people win to draw in customers, but not cost them too much for prizes. Which method fits this best?
4. Before they settled on a spinner game, they considered other things at their booth. Which of these suggestions would be considered chance experiments?


Learning Intentions and Success Criteria
- Compare probability models and observed frequencies
- Determine whether a given situation involving probability is a chance experiment
- Find or estimate probability using a model or data from a chance experiment
- Identify chance experiments
Cool-Down: What Affects Probability?
Match the description of the events to the most likely probability for that event to happen. A. B. C. D. 1. A short children’s book is opened to a random page; the probability that the page is numbered something between 1 and 10.
2. A long novel is opened to a random page; the probability that the page is numbered something between 21 and 31.
3. A long history book is opened to a random page; the probability that the page is numbered something between 1 and 100.
4. A dictionary is opened to a random page; the probability that the page is numbered 103.