Atividades de Cálculo 1A
Esta sequência de atividades foi desenvolvida na tentativa de facilitar o aprendizado dos conceitos acerca de derivadas de funções de uma variável. Sinta-se livre para percorrer este material no seu ritmo!
Neste material, não irei me aprofundar nos métodos e regras de derivação, uma vez que o objetivo deste é contextualizar e mostrar os conceitos que envolvem a derivada de uma maneira interativa e visual.
Observe o gráfico a seguir:
Observe que é possível alterar os valores da "a" e "b". Para tal, basta arrastar os controles deslizantes correspondentes. Mova os controles deslizantes e observe o que acontece com a reta no gráfico.
A partir dessas observações, responda:
Dada uma função , o que o coeficiente "a" controla? E o coeficiente "b"?
Se o coeficiente "a" é positivo, a função é:
Se o coeficiente "a" é negativo, a função é:
Se o coeficiente "a" é igual a zero, a função é:
Quando a função é constante, o gráfico da função é uma reta:
Observe o gráfico da função :
Responda com as suas palavras:
Para quais valores de , a função é positiva? E negativa?
Em qual valor de a função é igual a zero?
Se você não tivesse visto o gráfico, como obteria essas informações?
Em uma função afim, ou seja, uma função do tipo , faz sentido falarmos de inclinação, pois o gráfico da função é uma reta. No entanto, quando tratamos de outras funções, não podemos falar diretamente de inclinação.
A inclinação é um forte indicador para sabermos se uma função é crescente ou decrescente. Mas, se não podemos falar diretamente de inclinação em outros tipos de função, como determinamos se elas são crescentes ou decrescentes?
Observe, a seguir, o gráfico da função :
Observe que a função é crescente (sobe) e decrescente (desce) em diferentes intervalos.
Observe, a seguir, o gráfico da mesma função, mas, dessa vez, observe que traçamos uma reta tangente ao gráfico em diferentes valores de . Para alterar a posição da reta tangente, clique e arraste o "x" que está sobre o eixo x.
Após interagir com o gráfico acima, responda:
Quando a reta tangente à função é crescente (sobe), a função é:
Quando a reta tangente à função é decrescente (desce), a função é:
Quando a reta tangente à função é constante, a função é:
Observamos, anteriormente, que o gráfico de uma função do tipo é uma reta. Além disso, observamos que o coeficiente "a" dessa função determina se a função é crescente (sobe) ou decrescente(desce).
Observando que o comportamento de uma reta tangente à uma função nos diz sobre o comportamento da própria , seria interessante determinar qual é o coeficiente "a" dessa reta tangente.
Antes disso, observe no gráfico a seguir uma das formas de obter a equação de uma reta no plano cartesiano:
Note que, ao desenvolver a equação em destaque, o coeficiente que acompanhará a variável será . E que esse valor pode ser expresso como , onde é a variação em y e é a variação em x.
Então, se temos uma reta determinada pela função , podemos dizer que ou .
Vamos voltar para o gráfico da função . Agora, vamos tentar obter a reta tangente (em verde) em um ponto fixo . Mova o "x" que está sobre o eixo x.
Note que, à medida que um ponto se aproxima do outro, a reta roxa se aproxima da reta tangente. Quando um ponto sobrepõe o outro, as retas se sobrepõem. Voltando ao que estávamos tratando: qual é o coeficiente "a" da reta roxa?
Para calcular o coeficiente, basta lembrar que .
Neste caso, teremos que:
Para obter a reta tangente, basta que o ponto sobreponha o ponto . Ou seja, basta que . Mas teríamos um problema se substituíssemos diretamente:
Para que lidemos com este problema, teremos, então, que usar de limites! Ou seja, em vez de dizer que , vamos dizer que tende a . Desta forma:

Dizemos que este limite representa a derivada da função quando . E denotamos por . Ou seja:
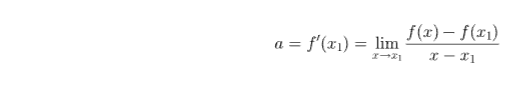
Sabendo disso, podemos afirmar que:
- Se , então e é crescente em ;
- Se , então e é decrescente em ;
- Se , então e não é crescente, nem decrescente e dizemos que tem um ponto crítico em .