Angles in the four quadrants (Unit circle)
Keywords
| Unit circle | 단위 원 | 単位円 (たんいえん) | 单位圆 (dānwèi yuán) |
| Trigonometric functions | 삼각 함수 | 三角関数 (さんかくかんすう) | 三角函数 (sānjiǎo hánshù) |
| Sine of 45 degrees | 45도의 사인 | 45度のサイン (45どのさいん) | 45度的正弦 (45 dù de zhèngxián) |
| Cosine of 45 degrees | 45도의 코사인 | 45度のコサイン (45どのこさいん) | 45度的余弦 (45 dù de yúxián) |
| Trigonometric identities | 삼각함수 정체성 | 三角恒等式 (さんかくこうとうしき) | 三角恒等式 (sānjiǎo héngděngshì) |
| Pythagorean theorem | 피타고라스의 정리 | ピタゴラスの定理 (ぴたごらすのていり) | 勾股定理 (gōugǔ dìnglǐ) |
| Radians and degrees | 라디안과 도 | ラジアンと度 (らじあんとど) | 弧度和度 (húdù hé dù) |
| Trigonometric equations | 삼각 방정식 | 三角方程式 (さんかくほうていしき) | 三角方程 (sānjiǎo fāngchéng) |
| Equilateral triangle | 정삼각형 | 正三角形 (せいさんかくけい) | 等边三角形 (děngbiān sānjiǎoxíng) |
| Right isosceles triangle | 직각 이등변 삼각형 | 直角二等辺三角形 (ちょっかくにとうへんさんかくけい) | 直角等腰三角形 (zhíjiǎo děngyāo sānjiǎoxíng) |
| Trigonometric ratios | 삼각비 | 三角比 (さんかくひ) | 三角比 (sānjiǎo bǐ) |
| Angle symmetry | 각도 대칭 | 角度の対称 (かくどのたいしょう) | 角度对称 (jiǎodù duìchèn) |
| Trigonometric exact values | 삼각함수의 정확한 값 | 三角関数の正確な値 (さんかくかんすうのせいかくなち) | 三角函数的精确值 (sānjiǎo hánshù de jīngquè zhí) |
| Quadrant | 사분면 | 象限 (しょうげん) | 象限 (xiàngxiàn) |
| Positive sine values | 양의 사인 값 | 正のサインの値 (せいのさいんのあたい) | 正弦值 (zhèngxián zhí) |
| Cosine values | 코사인 값 | コサインの値 (こさいんのあたい) | 余弦值 (yúxián zhí) |
| Angle opposite pairs | 각도의 반대 쌍 | 角度の対のペア (かくどのついのぺあ) | 角度的对偶对 (jiǎodù de duì'ǒu duì) |
Inquiry questions
| Factual Questions 1. What is the unit circle? 2. Calculate the sine and cosine of 45 degrees using the unit circle. 3. How is the unit circle used to define the trigonometric functions for all angles? 4. Identify the coordinates of the point on the unit circle corresponding to a 120-degree angle. 5. What are the values of sin and cos for the key angles on the unit circle (0, 30, 45, 60, 90 degrees)? | Conceptual Questions 1. Explain the significance of the unit circle in trigonometry. 2. Discuss how the unit circle relates to the Pythagorean theorem. 3. How do the concepts of radians and degrees apply to the unit circle? 4. Explain the relationship between the unit circle and the graphs of sine and cosine functions. 5. Compare the use of the unit circle in solving trigonometric equations to other methods. | Debatable Questions 1. Is the unit circle the most effective way to understand trigonometric functions? Why or why not? 2. Debate the importance of memorizing key points on the unit circle versus deriving from isoceles right triangle and the equilateral triangle. 3. Can the understanding of the unit circle be considered foundational for advanced mathematics? 4. Discuss the statement: "The unit circle simplifies the complexity of trigonometric functions." |

Moving into the other quadrants, we need to use the symmetry of the circle
2. Sine Waves: As we sail from 0° to 90°, the sine value climbs the rigging. How high does it reach at 90°? Now, plunge down to 270°—what happens to the sine value?
3. Reflective Waters: The applet shows that cos(160°) is about -0.94. If we reflect across the y-axis to 200°, does the cosine value change? What does this tell us about symmetry in the unit circle?
3. Reflective Waters: The applet shows that cos(160°) is about -0.94. If we reflect across the y-axis to 200°, does the cosine value change? What does this tell us about symmetry in the unit circle?
4. Quadrant Quest: Each quadrant holds its secrets. In which quadrants will you find positive sine values? And where will cosine lead us to positive shores?
5. Angle Amplification: Suppose we amplify our angle from 20° to 200°, passing through the stormy sea of the third quadrant. How does the sign of cosine and sine change?
6. Trigonometric Treasure: If cos(20°) is approximately 0.94, can we predict cos(160°) without a compass? Use the unit circle to verify your guess and find the value.
7. Full Circle: As we complete our 360° journey, can you predict the sine and cosine values at the cardinal points of 0°, 90°, 180°, and 270°? Confirm your predictions using the unit circle.
8. Opposite Odyssey: We know angles have opposite pairs on the unit circle. If the cosine of 20° is 0.94, what's the cosine of its opposite angle? Use the unit circle to find out!
9. Sine and Cosine Saga: Create your own angle and predict its sine and cosine values. Then, embark on a quest to find an angle in a different quadrant with the same sine value.
10. Circle of Life: The unit circle is never-ending. If you keep adding 360° to an angle, what happens to the sine and cosine values? Do they change or remain steadfast like the North Star?
Part 2 - The unit circle exact values
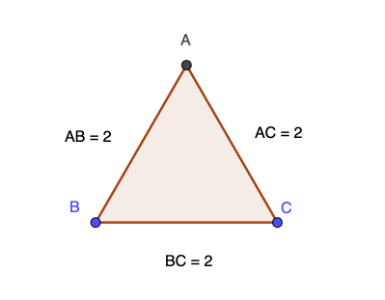
Activity 1: Finding sin(60°), cos(60°), and tan(60°) 1. **Draw an equilateral triangle** with side length 2 (for simplicity). Label the vertices A, B, and C. 2. **Draw the altitude** from vertex A to the midpoint of the base BC, creating two 30°-60°-90° right triangles. Let's call the midpoint D. 3. **Determine lengths** of AD, BD, and AB. Since AB = 2, and BD = 1 (half of AB), use Pythagoras' theorem to find AD. 4. **Calculate trigonometric ratios** for 60° using the right triangle ABD.
Activity 2: Finding sin(30°), cos(30°), and tan(30°) 1. Using the same triangle, **apply the trigonometric functions** to angle BAD (30°). 2. **Calculate** the sine, cosine, and tangent of 30° using the lengths found in Activity 1.
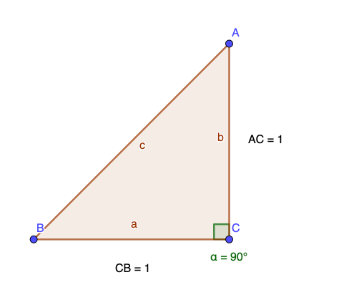
Activity 3: Finding sin(45°), cos(45°), and tan(45°) 1. Draw a right isosceles triangle** with the two legs of equal length. For simplicity, let each leg have a length of 1. 2. Label the hypotenuse** and calculate its length using Pythagoras' theorem. 3. Calculate trigonometric ratios** for 45° using the lengths of the legs and the hypotenuse.
![[MAA 3.5] SIN, COS, TAN ON THE UNIT CIRCLE - IDENTITIES.pdf](https://www.geogebra.org/resource/hdaf2m4w/1JWVNxwj7C3utPMV/material-hdaf2m4w-thumb.png)
![[MAA 3.5] SIN, COS, TAN ON THE UNIT CIRCLE - IDENTITIES_solutions.pdf](https://www.geogebra.org/resource/pnudcr2c/U6ULZmfhHEGvtE7c/material-pnudcr2c-thumb.png)

