Intersecting chord theorem
Introduction
Intersecting chord theorem states that when two chords in a circle intersect each other, the products of the length of the lines between the point on circle and intersecting point is equal.
AB=CD
A,B,C and D are the lengths of the lines between the intersecting point of the chords and their points on circle.
No matter where the intersecting point is, the products would always be equal.
Proofing
1.
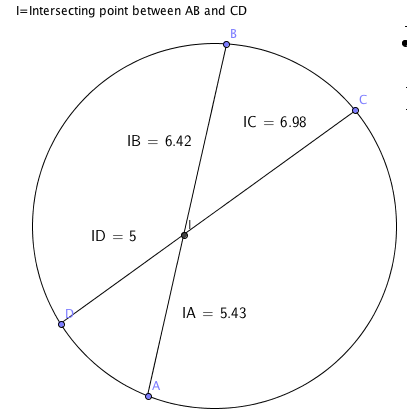
(Note: Lengths on diagram are rounded off for clarity and calculations may be slightly off when displayed values are entered into a calculator.)
According to the intersecting chord theorem, this statement should be correct (IA)(IB)=(IC)(ID)
Lets find out.
(IA)(IB)=(5.43)(6.42)=34.9(3 s.f.)
(IC)(ID)=(6.98)(5)=34.9(3 s.f.)
This shows us that the statement is correct.
2.

(Note: Lengths on diagram are rounded off for clarity and calculations may be slightly off when displayed values are entered into a calculator.)
Heres another example
(IA)(IB)=(IC)(ID)
(IA)(IB)=(0.91)(3.51)=3.20(3 s.f.)
(IC)(ID)=(0.36)(8.89)=3.20(3 s.f.)
Here's a tool to help you visualise the intersecting chord theorem. There is also a calculator function.
Drag the sliders to shift the four different points on the circle.
Question 1
Carl just moved into his new house. He has a choice between two routes to get to school, there are two pathways on each side of a circular field that has a fence running straight through the diameter of it. The pathways intersect each other at different points which are i and j. Carl wants to find the shorter route to get to school but he only has certain lengths of the pathways. Help him find the shorter path.
Diameter=HS=1100m
Hi=200m
Ui=150m
Oj=300m
jS=450m
jK=250m
Not drawn to scale
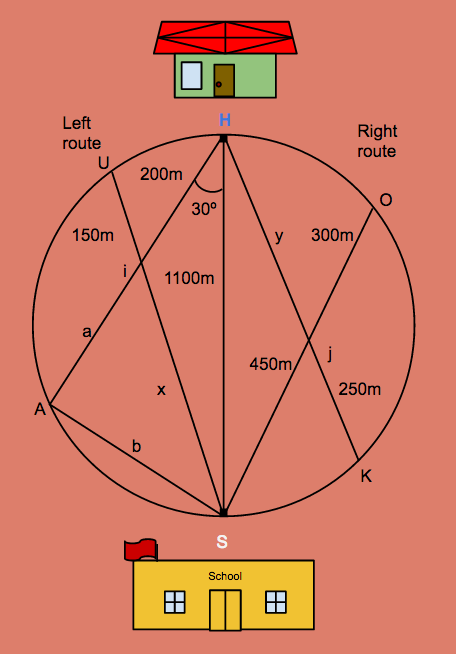
Solution+Marking scheme
y=450x300/250-----------------[M1]
=540
Right route=450m+540m-----[M1]
=990m
The right route took 990m
b=sin(30)=½
sin(30)=b/1100
b=1100/2
=550-----------------------------[M1]
HA=
=952.63(2d.p.)
a=952.628-200
=752.63(2d.p.)
x=752.63x200/150
=1003.50-----------------------[M1]
Left route=1003.50+200
=1203.50(2d.p.)
The left route took 1203.50m while the right route took 990m.
The right route was shorter.-[A1]
Euclid's Theory
Euclid's Theory states that the shortest distance between two points is a straight line connecting them. This is very true as no matter what shape or size any objects or points are the shortest distance connecting them on a one dimensional plane is still a straight line. This can be very helpful in helping us narrow down distances, for example, someone on the other side of the earth would be 20,000km away from me if I were to have to travel along earth's circumference but in actual reality he is only 12,000km away from me which is the earth's diameter. Another example would be two walkie-talkies, it does not matter if the path between the two walkie-talkies have obstacles that need some sidetracking to overcome as long as the walkie-talkies are within their certain range of operation which is measured by the shortest distance between them they would work.