Lineare Vektorfelder: die Formeln
Diese Seite ist Teil des geogebra-books Moebiusebene.
Ist irgendein Geradenvektor, so wird durch- für alle Berührgeradenvektoren
auf der Möbiusquadrik ein lineares Vektorfeld erklärt. Je nach dem Typ von besitzen diese Vektorfelder eine oder zwei Nullstellen: eine, falls selber eine Berührgerade ist, zwei, wenn das komplexe Vielfache einer Schnittgeraden ist. Die Nullstellen sind die Pole der "Infinitesimalen Bewegung" . Diese Bezeichnung erklärt sich aus dem Zusammenhang zwischen der LIE-Algebra und der LIE-Gruppe .
Gesucht sind die Lösungskurven (Integralkurven) dieser linearen Vektorfelder.
Hierzu erklären wir zunächst für jedes die bezüglich schiefe Abbildung:
und damit die Exponentialabbildung
Man kann allgemein zeigen, dass für alle eine gleichsinnige Möbiusabbildung ist, dh. in liegt. Wir identifizieren jedoch jede dieser Abbildungen direkt als gleichsinnige Möbiusabbildung und zeigen zudem, dass surjektiv ist: jede gleichsinnige Möbiusabbildung ist das Bild einer Infinitesimalen unter der Exponentialabbildung.
Fall 1: ist ein Berührgeradenvektor: . Wir wählen ein euklidisches Koordinatensystem mit . Damit ist das zugehörige lineare Vektorfeld.
Nach den Vertauschungsregeln des euklidischen Koordinatensystems (s.u) erhält man:
-
mit reellem oder komplexem t.
ist also in diesem KOS eine Verschiebung um das reelle oder komplexe t.
- Die Kurve ist eine W-Bewegung in , das ist eine Ein-Parameteruntergruppe.
- Die Kurve ist eine W-Kurve und eine Integralkurve des Vektorfeldes, in diesem KOS eine Gerade durch .
Fall 2: Ist , so wählen wir das euklidische KOS so, dass gilt.
Dann ist das zugehörige lineare Vektorfeld.
Wieder mit den Vertauschungsregel des euklidischen KOS ergibt sich
- Erneut ist die Kurve in eine W-Bewegung .
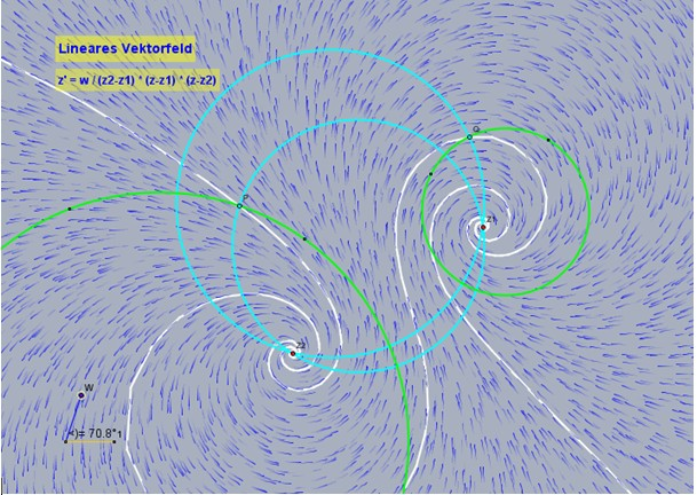
- Die Kurve ist eine W-Kurve und eine Integralkurve des Vektorfeldes durch , im gewählten KOS handelt es sich je nach dem Argument von um eine logarithmische Spirale, eine Ursprungsgerade oder einen um den Ursprung konzentrischen Kreis.
Die Umrechnungsformeln für euklidische Koordinatensysteme:
Das Vektorfeld unten wurde mit Cinderella.2 erstellt, hier nur als Bild, im Original ziemlich beweglich!