Lugares geométricos 4
Figura 1
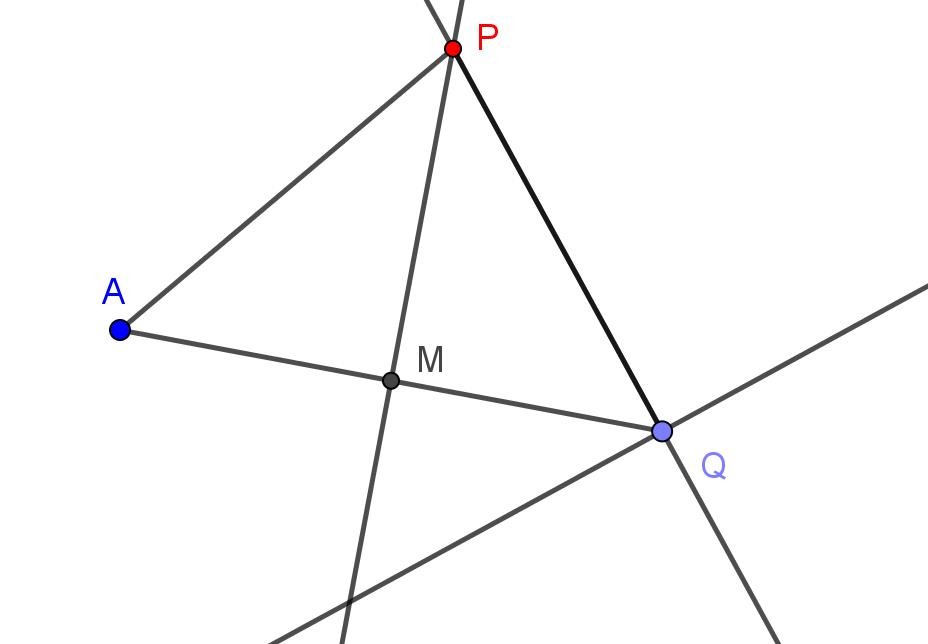
a) Arrastre el punto Q y observe la trayectoria que sigue el punto P, describa la curva que traza el punto P al arrastrar Q.
b1) Magnitudes que permanecen fijas
b2. Magnitudes que varían
c) Entre las magnitudes que están variando, ¿cuáles permanecen iguales entre sí, a pesar de la variación?
d) Investigue cuál es la definición de parábola como lugar geométrico y argumente con base en el comportamiento de las magnitudes de la construcción (Figura 1), por qué la curva trazada por P al arrastrar Q, es efectivamente una parábola.
a) Arrastre el punto Q y observe los triángulos AOQ y QMP, estos triángulos cambian al mover el punto Q, pero conservan algunas características. Describa cuáles son las características que conservan.
b) Al arrastrar el punto Q, los lados de los triángulos AOQ y QMP varían, excepto el lado AQ, ¿por qué?
c) Los triángulos AOQ y QMP se conservan semejantes al mover Q. Ofrezca una justificación geométrica de esta semejanza.
d) Exprese la hipotenusa AQ en términos de a y t.
e) Exprese MQ en términos de a y t. Use para ello el hecho de que M es el punto medio de AQ, ¿por qué M se mantiene como punto medio de AQ?
f) Use la semejanza de los triángulo AOQ y QMP para establecer una relación algebraica entre las variables s y t.
a) Simplifique esta ecuación lo más que pueda y escríbala aquí:
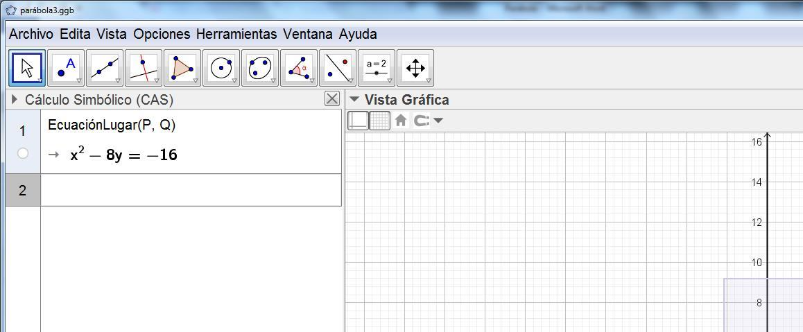
Compare la simplificación de la ecuación que usted ha obtenido y compárela con la que arroja GeoGebra, ¿cuál es la diferencia?
c) La ecuación representa algebraicamente la parábola que hemos trazado. Haga x=0 en esta ecuación y resuelva la ecuación para obtener el valor de y. ¿Qué significa este valor en la gráfica?
d) Ahora haga y=0 en la ecuación y trate de resolver la ecuación ¿Qué significado gráfico tendrá la inexistencia de raíces reales para esta ecuación?