I punti di non derivabilità
Abbiamo definito la derivata come limite per del rapporto incrementale:
In questo capitolo ci poniamo il problema del caso in cui questo limite NON esiste, ovvero i punti in cui NON riusciamo a calcolare il limite, e quindi in cui la derivata NON esiste. Tali punti si dicono punti di non derivabilità. Nella seguente animazione ricapitoliamo il concetto di derivata e vediamo i vari casi di non derivabilità. Il primo obiettivo è quello di approfondire il concetto di derivata e verificarne la nostra comprensione; vedremo in seguito che queste considerazioni hanno anche un'utilità pratica.Riassumiamo quanto visto finora:
1) Una funzione si dice derivabile in un punto se il risultato della sua funzione derivata è definito nel punto ed assume un valore FINITO (cioè non ).
Possiamo verificare che una funzione NON è derivabile in due modi:
- osservando che il punto NON appartiene al dominio della sua derivata (ma deve appartenere al dominio della funzione: se la funzione non esiste non ha neppure senso chiedersi di quanto è inclinata o con quale velocità sta aumentando o diminuendo). La derivata della funzione non esiste quindi in , che è quindi un punto di non derivabilità. Per capire di quale tipo di punto si tratti studiamo il limite per della derivata.
- nel caso il limite del rapporto incrementale della funzione (che è la derivata) non sia definito in quel punto, ad esempio perché il suo limite sinistro (, cioè l'incremento su cui calcolo la velocità media è positivo e disegnato alla sinistra del punto) e quello destro (, incremento negativo e disegnato alla destra del punto) non coincidono.
- Se la derivata non esiste in , ed il suo limite sia destro che sinistro per tende a oppure a abbiamo un punto di flesso verticale.
- Se la derivata non esiste in , ed i suoi limiti destro e sinistro per tendono uno a e l'altro a abbiamo un punto di cuspide.
- Se il limite destro e sinistro della derivata, cioè del rapporto incrementale hanno due valori FINITI ma differenti tra loro abbiamo un punto a cui la funzione "giunge" da sinistra con una certa inclinazione e "riparte" verso destra con un'inclinazione diversa: non è possibile definire quindi LA inclinazione in quel punto (la derivata non esiste) ed abbiamo un punto angoloso.
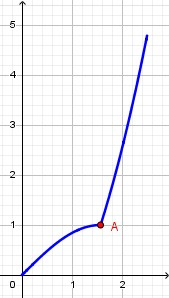
Nella funzione in esempio, i punti angolosi erano punti di estremi relativi della funzione. Nella figura sotto puoi vedere però che un punto angoloso non è necessariamente anche un punto di estremo relativo, e quindi va valutato caso per caso.