Linear Equation
What are lines made of?
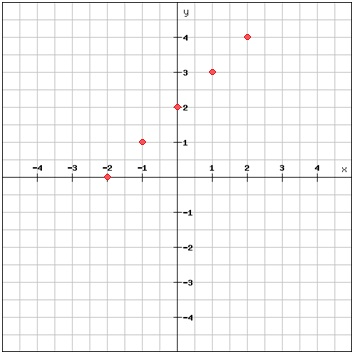
Lines are collections of points
Earlier we talked about how a bunch of points can make a line. We had x-coordinates and y-coordinates determining where these points go, and the equation of the line tells us how the x-coordinate and y-coordinate of the (x, y) pairs are related.
Slope-Intercept Form of a Line
A "line" is the solution of an equation between two variables, usually we use x and y. This equation describes a relationship between x and y. Because this equation stays the same, if we change the variable x, its "partner" y also changes.
A line equation usually looks like y = mx + b. The variables are y and x, and the letters m and b tell us what the relationship between the variables looks like.
This form of a line equation is called "slope-intercept form".
In this form, m is the "slope" and b is the "intercept". Intercept--that word kind of sounds like "intersect". This number tells us where the line crosses the y-axis.
Our Line: y = mx + b
Instructions & Questions
1. Play with the sliders for the value of m and b.
2. What happens when you make m very big? What about very small?
3. What happens when you make b very big? Very small?
4. What kind of number does m need to be to make the line seem "uphill"? What about "downhill?"
5. Why do you think m is called the "slope" of a line? Why do you think b is called the "intercept" of a line? (Hint: think about the word "intersect").
What you need to do:
Type or write down your answers to questions 2, 3, 4, & 5 above. Email them to Miss Shedd, sshedd@greeleyschools.org, message them to Miss Shedd on Schoology, or bring your paper that has the answers written on it to class on Tuesday.
If you email them or message them, please make sure to put your first and last name in the message or the subject. Please use your school email address.