¿Tiene solución el problema planteado?
Observando el grafo obtenido de la ciudad de Königsberg y calculando el grado de todos sus vértices:
Vértice o nodo Grado A 5 B 3 C 3 D 3Vemos que hay tres vértices con grado y un vértice con grado
. Es decir, no hay ninguno con grado par. Por tanto, según el teorema anterior, este grafo no contiene un camino Euleriano, esto es, no podemos comenzar en un punto de la ciudad y recorrer cada uno de los puentes sólo una vez y terminar en el punto de partida.
Aún modificando la cantidad de puentes o caminos, se puede verificar, que realmente es únicamente posible completar el ciclo Euleriano cuando existen 0 o 2 nodos con grado impar, y en caso que hayan 2 de esos nodos, deben ser los puntos de comienzo y fin del recorrido:
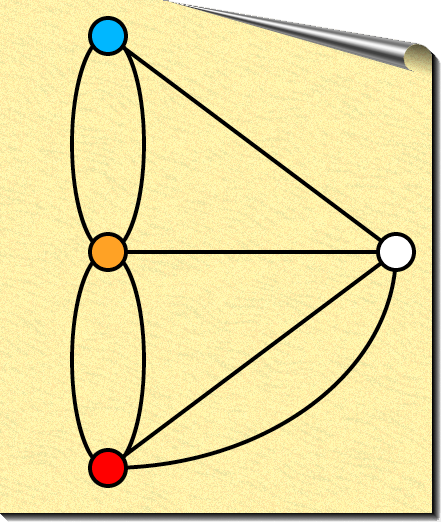
Como se puede verificar, el agregar un octavo puente se convierte en la solución del problema puesto que ahora existen 2 nodos con grado impar (el Naranja y el Azul), que permiten crear caminos Eulerianos comenzando o terminando en esos nodos.