Area of a Polygon
- Author:
- Ku, Yin Bon (Albert)
- Topic:
- Area
Suppose you are given a square. Of course it is easy to determine its area by taking square of the length of its side. However, it is much harder to find the area of an irregular shape.
Here we consider any polygon and try to find its area.
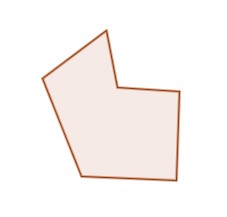
Euclid's idea is very simple - construct a square whose area equals the area of this polygon.
But how to do it? We can first cut the polygon into triangles.
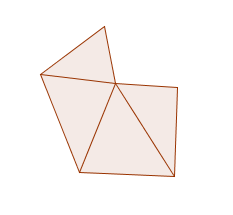
Then for each of these triangles, we can construct a parallelogram with a fixed base length and angle such that it has the same area as that of the triangle. Stacking up all these parallelogram to form a big parallelogram.
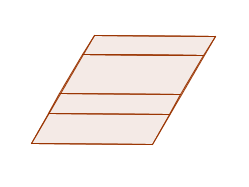
The last step is to construct a square whose area equals the area of the big parallelogram.