SOH-CAH-TOA
Intro
We all know the identities SOH-CAH-TOA.
But how do these come to be?
Let's first take a look at the unit circle.
Sine and Cosine
How did we create the functions sine and cosine?
To figure this out let take a look at the two unit circles.
How is the length of BD related to the y-coordinate of B? related to the sine of a (shown at bottom of legend)?
How is the length of AD related to the x-coordinate of B? related to the cosine of a (shown at bottom of legend)?
What about a "non"-unit circle?
Think about these given circles.
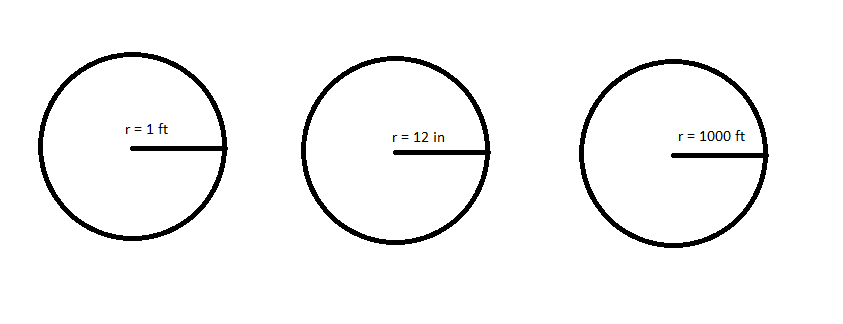
What is the measure of each radius in inches? feet? radii?
Which is a unit circle?
What if we wanted sine/cosine in radii?
To get sine in terms of radii, we would have to convert the length of sine (BC) to radii.
You can do a similar thing with cosine.
What is the relationship between this length and the sine/cosine of the angle.
So in order to find sine/cosine you have to divide the vertical/horizontal height (opposite/adjacent) by the radius. But hey! the hypotenuse of the triangle is equal to the radius. This is how we get:

 How can we extend this to tangent?
The tangent happens to be the slope of line AB. Using the slope formula, we can see, if:
then the the slope of AB is:
How can we extend this to tangent?
The tangent happens to be the slope of line AB. Using the slope formula, we can see, if:
then the the slope of AB is: