Gradiente
Sea una función de x y y, diferenciable y continua tal que y existen. Entonces el gradiente de f, se denota con , y es igual a:
se lee "nabla de f". Otra notación es grad f(x, y). En el ejemplo de abajo, se puede notar que el vector gradiente puede ubicarse perpendicular a la curva de nivel en un punto determinado.
Gradiente
Ejemplo 2
En Matlab u Octave
%Preparación de la superficie a graficar
[X,Y] = meshgrid(-2:.2:2);
Z = X.*exp(-X.^2 - Y.^2);
%Definición del conjunto de gradientes
[DX,DY] = gradient(Z,.2,.2);
figure
%curvas de nivel
contour(X,Y,Z)
hold on
%gradiente
quiver(X,Y,DX,DY)
hold off
%superficie
figure
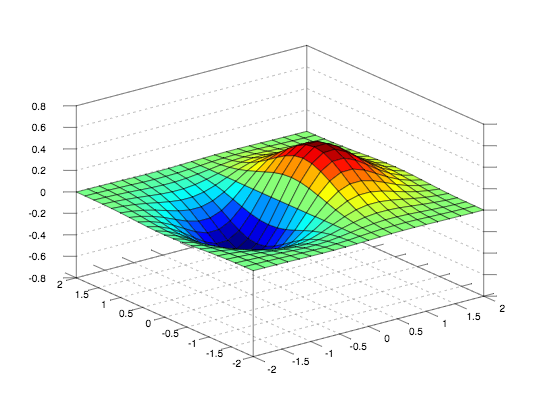
surf(X,Y,Z)
Superficie
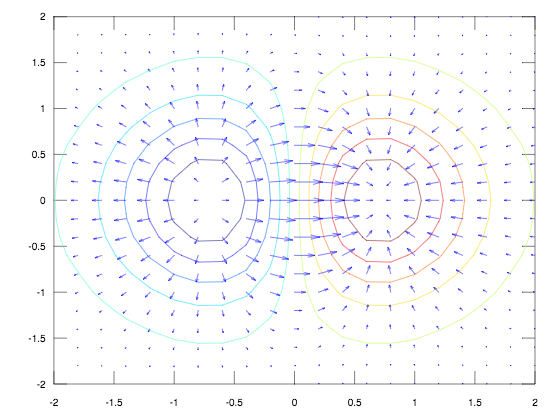
Curvas de nivel y Campo de vectores gradiente
Propiedades del Gradiente
La dirección de máximo incremento de f está dado por .
La dirección de mínimo incremento de f está dado por