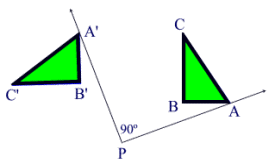
Rotation
Rotations
This image shows an example of a rotation of 90 degrees around the origin, or point D on this graph. Point D is the center of rotation, which means that it is what the pre-image (in blue) rotates around a certain amount of degrees to get to the image (in red). I can check that the rotation is accurate by using the rule that when you rotate a pre-image 90 degrees counter-clockwise, you change the coordinates from (x,y) to (-y,x). Using the example on the graphs, we can prove this is true. Take point A for example. It's coordinates are (4,1). When you apply the rule to the coordinates, it becomes (-1, 4), and that is the coordinates of A' on the graph, so we know that the rotation was done correctly. The same can be done for points B and D.