Struktur des Buches
Mit Hilfe moderner Mathematiksoftware können sehr viel mehr geometrische Sachverhalte überzeugend
dargestellt werden, als das früher möglich war. Wir wollen möbiusgeometrische Beziehungen und Objekte
visualisieren und dabei vermeiden, das die Schönheit der Geometrie hinter einer Fülle von Formeln
versteckt bleibt.
Natürlich müssen Aussagen bewiesen werden; wie weit die Beweise ins Detail gehen müssen, hängt jedoch
auch vom Betrachter ab. Ein Großteil der Begründungen fundiert auf Sätzen aus der Linearen Algebra:
es geht um quadratische, symmetrische oder alternierende Formen, um selbstadjungierte Abbildungen,
Dualität, Polarität. Für Experten auf diesem Gebiet erschließen sich manche Sachverhalte aus den Bildern,
für andere versuchen wir die Begründungen bereitzustellen.
Als Grundmuster des Buches versuchen wir, Sachverhalte durch Bilder erfahrbar und verstehbar zu machen,
Begründungen werden als solche gekennzeichnet.
Manche Beweise erscheinen uns selber als unbefriedigend kompliziert: vielleicht bringen die Bilder Leser
und Betrachter auf erhellendere Ideen.
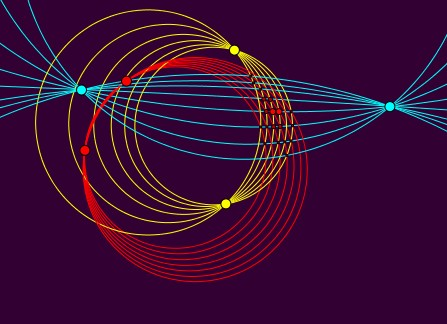
Bilder können jedoch auch täuschen, daher sind Beweise unabdingbar: es gibt zum Beispiel Konstruktionen
aus drei Kreisbüscheln, die ein Sechseckgewebe vortäuschen, welches in Wahrheit keines ist!
Obwohl beim Berechnen der Schnittpunkte von Kreisen sich häufende Rundungsfehler ergeben, kann ein
aus den Kreisen von Kreisbüscheln konstruiertes "Sechsecknetz" über viele Lagen hinweg stabil erscheinen,
erst am Rand wird erkennbar, dass die Sechsecknetzbedingung nicht mehr gilt. Und dann ist nicht sicher,
ob es eine Folge der Rundungsfehler ist, oder ob die Sechseckbedingung von Anfang an nicht gilt!
Das Bild unten: KEIN Sechseckgewebe!
Diese Seite ist Teil des GeoGebra-Books Moebiusebene.