PROBLEMS WITH CIRCLES
Instructions
Use GeoGebra to help you construct models of these problems and then find solutions. Use a calculator as necessary.
Problem 1.
Anne is riding a horse which is tied to a pole with a 4 m piece of rope and her friend Laura is riding a donkey which is 2 m from the same center point. They both ride 10 times around the circles. Who will travel farther? How much farther? Use GeoGebra to construct a model that will help you solve this problem. Print your construction and on the printout write your answers and briefly explain/show how you solved the problem.
Problem 2.
The rope that attaches a tire swing to a tree is 4 m long. At its maximum, the swing travels 108°. Calculate the distance traveled by the tire when the swing angle is at its maximum. Use GeoGebra to construct a model that will help you solve this problem. Print your construction and on the printout write your answer and briefly explain/show how you solved the problem.
Problem 3.
In a city park, a circular fountain with a diameter of 10 meters lies alone in the center of a stone-filled, circular pad with a diameter of 40 meters. New gravel is needs to be ordered to fill the space around the fountain. The area of the stone-filled space is needed to order the gravel. Also, new edging material is need to keep the gravel in place – how much should be ordered? Use GeoGebra to construct a model of the problem, and then use your construction to help you calculate the necessary measurements. Print your construction and on the printout write your answer and briefly explain/show how you solved the problem.
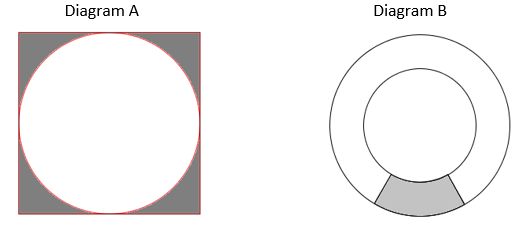
Problem 4.
See Diagram A below. Use GeoGebra to construct and calculate the total area of the shaded sections, knowing that the side of the outer square is 6 cm and the radius of the circle is 3 cm. Print your construction and on the printout write your answer and briefly explain/show how you solved the problem.
Problem 5.
See Diagram B below. A circular garden is being constructed. The landscaper needs to know the area of the shaded section of the garden. The two concentric circles have a radius of 8 meters and 5 meters. If the straight line sides of the shaded area are extended to the center of the circles, the angle is 60°. Use GeoGebra to construct a model of the problem, and then use your construction to help you calculate the area of the shaded circular trapezoid. Print your construction and on the printout write your answer and briefly explain/show how you solved the problem.
Problem 6.
A central angle of 40° is plotted on a circle with a 4 meter radius. You need to calculate the area of the circular segment between the chord joining the ends of the two radii and its corresponding arc. Use GeoGebra to construct a model of the problem, and then use your construction to help you calculate the area of the shaded circular trapezoid. Print your construction and on the printout write your answer and briefly explain/show how you solved the problem.