Animated SIN Functions
Overview:
Using GeoGebra and Desmos, we created various sin functions that have different unknown variables that have sliders. These sliders can move around from a value of -5 to +5. When animating them, we can see the different effects each different variable has on the sin functions. Below is a video where we have all of the sliders going at the same time.
The videos shows the sliders moving from -5 to +5 creating a wave motion that students can analyze at each point in the slider. Here students can make conjectures based on what they see with regards to each variable and each slider.
30-1

Along with that, 30-1 Trigonometry applies to the curriculum specifically number 3. Students need to solve problems using the trigonometric ratios.
Students should be able to:
- Determine, with technology, the approximate value of a trigonometric ratio for any angle with a measure expressed in either degrees or radians.
- Determine, using a unit circle or reference triangle, the exact value of a trigonometric ratio for
angles expressed in degrees that are multiples of 0º, 30º, 45º, 60º or 90º, or for angles
expressed in radians that are multiples of or , and explain the strategy.
- Determine, with or without technology, the measures, in degrees or radians, of the angles in a
specified domain, given the value of a trigonometric ratio.
- Explain how to determine the exact values of the six trigonometric ratios, given the
coordinates of a point on the terminal arm of an angle in standard position.
- Determine the measures of the angles in a specified domain in degrees or radians, given a
point on the terminal arm of an angle in standard position.
- Determine the exact values of the other trigonometric ratios, given the value of one
trigonometric ratio in a specified domain.
- Sketch a diagram to represent a problem that involves trigonometric ratios.
- Solve a problem, using trigonometric ratios.
30-1

Also in 30-1 Relations and Functions applies to the curriculum specifically numbers 2-5. Students must have a basic understanding of the transformations on a specific function.
30-3
Sample Questions:
Grade 12:
Write down what they are seeing with regards to each variable. Change only one variable at a time and see what happens. Notice what happens with positive and negative numbers in the formula.
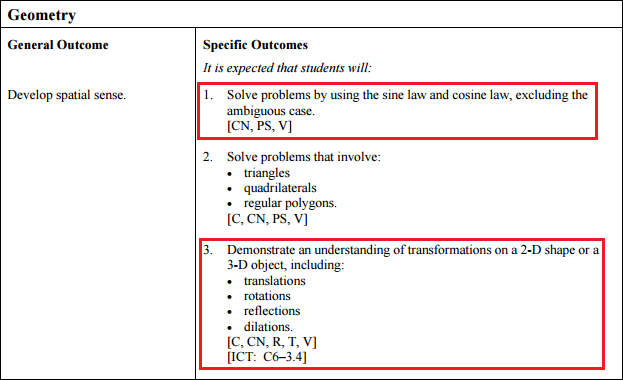
Lastly, the 30-3 Geometry part of the curriculum specifically number 1 and 3 apply. Students need to use this knowledge to solve problems using the laws of sine and cosine and they must understand the translations, rotations, reflections and dilation's that can occur to a sine or cosine function.
Conclusion:
I really like both programs to see the differences in the sine functions. GeoGebra and Desmos both gave the options of sliders which makes it easy to press the play button and watch what happens to each function as the variable changes. I would use them both in my classroom as an introduction to the transformations of the trigonometric functions.