La rifrazione della luce-modello ondulatorio
La rifrazione della luce-modello ondulatorio
Abbiamo visto che la teoria
corpuscolare spiega molti dei fatti osservati e noti ai tempi di Newton. La
teoria ondulatoria è anch'essa in grado di farlo? Consideriamo le domande alle
quali la teoria corpuscolare ha già risposto, al fine di valutare se la teoria
ondulatoria risponde altrettanto bene.
Con lo scopo di evidenziare
una corrispondenza tra i fenomeni luminosi e i fenomeni di tipo ondulatorio,
faremo riferimento ad uno strumento
capace di generare impulsi ondulatori bidimensionali e macroscopici, ovvero
onde la cui ampiezza sia osservabile a occhio nudo: a tale scopo è stato
progettato l'ONDOSCOPIO sul quale possono essere generate onde sinusoidali di
forma rettilinea (a fronte d’onda piano) o circolare (a fronte d’onda
circolare).
LA RIFRAZIONE
 Per quanto riguarda le onde
meccaniche, la rifrazione può essere osservata su un ondoscopio. Occorre
semplicemente trovare il modo per realizzare il passaggio di un’onda piana da un mezzo di propagazione ad
un altro. Si può ottenere, ad esempio, modificando la profondità
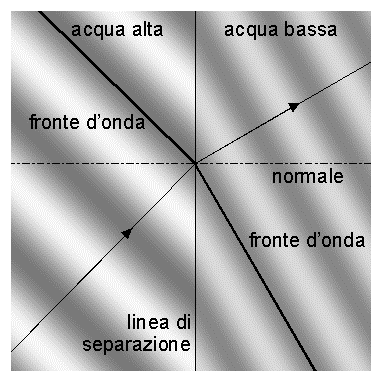
dell’acqua. Il risultato è quello che si osserva nel disegno a fianco. In acqua
bassa le onde vanno più piano e perciò, per garantire continuità al fronte
d’onda devono “piegarsi”, modificando la direzione di propagazione.
Interessante è pure il fatto
che a distinguere un mezzo
di propagazione dall’altro è la velocità di propagazione delle onde e, riferito
alla luce, questo deve avere a che fare con l’indice di rifrazione
Per quanto riguarda le onde
meccaniche, la rifrazione può essere osservata su un ondoscopio. Occorre
semplicemente trovare il modo per realizzare il passaggio di un’onda piana da un mezzo di propagazione ad
un altro. Si può ottenere, ad esempio, modificando la profondità
dell’acqua. Il risultato è quello che si osserva nel disegno a fianco. In acqua
bassa le onde vanno più piano e perciò, per garantire continuità al fronte
d’onda devono “piegarsi”, modificando la direzione di propagazione.
Interessante è pure il fatto
che a distinguere un mezzo
di propagazione dall’altro è la velocità di propagazione delle onde e, riferito
alla luce, questo deve avere a che fare con l’indice di rifrazione
 v sempre minore o uguale a c, la quale è la massima
velocità possibile (relatività di Einstein)
n è una proprietà fondamentale dei mezzi materiali
trasparenti (e più misurabile rispetto alla v!)
L’indice di rifrazione n può variare con la lunghezza
d’onda: onde luminose di lunghezza d’onda maggiore hanno n minore e viceversa.
(http://www00.unibg.it/dati/corsi/208406/6847-Lezione14.pdf)
Vediamo ora come
la teoria ondulatoria spiega il fenomeno della rifrazione della luce sulla base
del principio di Huygens. Costruiamo, quindi, il raggio rifratto con il
metodo dell'inviluppo piano.
Consideriamo due mezzi in cui la luce si propaga
rispettivamente con velocità v1 e v2 (per il momento
supponiamo v1>v2).
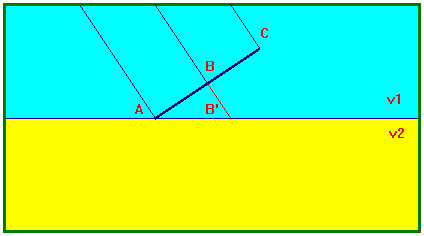
Consideriamo poi un'onda piana che si muove nel mezzo con
velocità v1, tre raggi d'onda e un fronte d'onda, AC, che comincia
ad incontrare la superficie di separazione dei due mezzi nel punto A.
v sempre minore o uguale a c, la quale è la massima
velocità possibile (relatività di Einstein)
n è una proprietà fondamentale dei mezzi materiali
trasparenti (e più misurabile rispetto alla v!)
L’indice di rifrazione n può variare con la lunghezza
d’onda: onde luminose di lunghezza d’onda maggiore hanno n minore e viceversa.
(http://www00.unibg.it/dati/corsi/208406/6847-Lezione14.pdf)
Vediamo ora come
la teoria ondulatoria spiega il fenomeno della rifrazione della luce sulla base
del principio di Huygens. Costruiamo, quindi, il raggio rifratto con il
metodo dell'inviluppo piano.
Consideriamo due mezzi in cui la luce si propaga
rispettivamente con velocità v1 e v2 (per il momento
supponiamo v1>v2).
Consideriamo poi un'onda piana che si muove nel mezzo con
velocità v1, tre raggi d'onda e un fronte d'onda, AC, che comincia
ad incontrare la superficie di separazione dei due mezzi nel punto A.

 Il punto A comincia ad emettere onde sferiche elementari che si propagano nel
secondo mezzo. Mentre queste onde avanzano, i restanti punti del fronte d'onda
continuano a viaggiare nel primo mezzo, incontrando la superficie di
separazione dei due mezzi in tempi successivi. Poiché le velocità di
propagazione sono diverse, le distanza percorse, a parità di tempi, saranno
diverse: quando il punto B raggiunge la superficie di separazione in B', l'onda
secondaria emessa da A avrà percorso un tratto di lunghezza inferiore a BB'.
Il punto A comincia ad emettere onde sferiche elementari che si propagano nel
secondo mezzo. Mentre queste onde avanzano, i restanti punti del fronte d'onda
continuano a viaggiare nel primo mezzo, incontrando la superficie di
separazione dei due mezzi in tempi successivi. Poiché le velocità di
propagazione sono diverse, le distanza percorse, a parità di tempi, saranno
diverse: quando il punto B raggiunge la superficie di separazione in B', l'onda
secondaria emessa da A avrà percorso un tratto di lunghezza inferiore a BB'.
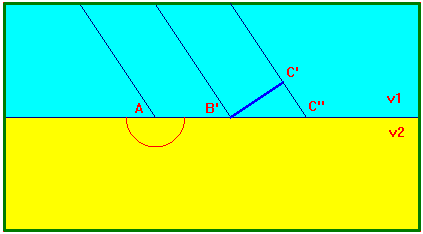
 A questo punto anche B' comincia ad emettere onde, mentre l'onda emessa da A
continua ad avanzare, ed il punto C' del fronte d'onda viaggia, nel primo
mezzo, fino ad incontrare la superficie di separazione in C''. Quando C' sarà
arrivato in C'', le onde emesse da A e B' avranno l'aspetto in figura.
A questo punto anche B' comincia ad emettere onde, mentre l'onda emessa da A
continua ad avanzare, ed il punto C' del fronte d'onda viaggia, nel primo
mezzo, fino ad incontrare la superficie di separazione in C''. Quando C' sarà
arrivato in C'', le onde emesse da A e B' avranno l'aspetto in figura.
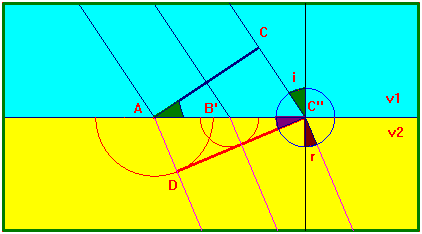
 Secondo il principio di Huygens la superficie d'onda rifratta sarà l'inviluppo di tutte le superfici d'onda
secondarie emesse dai punti che successivamente incontrano la superficie di
separazione tra i due mezzi. I raggi d'onda rifratti saranno perpendicolari al
fronte d'onda rifratto, come mostrato nella figura.
Allora l'inviluppo dopo il tempo Dt avrà
cambiato direzione di propagazione.
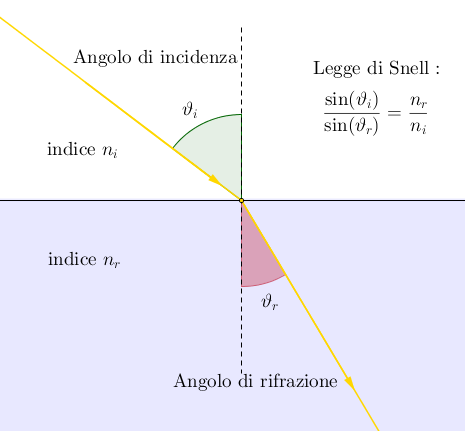
Non solo il modello ondulatorio prevede la rifrazione, ma da esso si
deduce pure la legge di Snell della rifrazione:
Secondo il principio di Huygens la superficie d'onda rifratta sarà l'inviluppo di tutte le superfici d'onda
secondarie emesse dai punti che successivamente incontrano la superficie di
separazione tra i due mezzi. I raggi d'onda rifratti saranno perpendicolari al
fronte d'onda rifratto, come mostrato nella figura.
Allora l'inviluppo dopo il tempo Dt avrà
cambiato direzione di propagazione.
Non solo il modello ondulatorio prevede la rifrazione, ma da esso si
deduce pure la legge di Snell della rifrazione:
 dove nr e ni sono le velocità del raggio nei mezzi r e i
raggio più lento → traiettoria più vicina alla normale (e
viceversa)
La frequenza dell’onda rimane invariata
La lunghezza d’onda diminuisce se n diminuisce, o aumenta
se n aumenta
dove nr e ni sono le velocità del raggio nei mezzi r e i
raggio più lento → traiettoria più vicina alla normale (e
viceversa)
La frequenza dell’onda rimane invariata
La lunghezza d’onda diminuisce se n diminuisce, o aumenta
se n aumenta
 Per quanto riguarda le onde
meccaniche, la rifrazione può essere osservata su un ondoscopio. Occorre
semplicemente trovare il modo per realizzare il passaggio di un’onda piana da un mezzo di propagazione ad
un altro. Si può ottenere, ad esempio, modificando la profondità
dell’acqua. Il risultato è quello che si osserva nel disegno a fianco. In acqua
bassa le onde vanno più piano e perciò, per garantire continuità al fronte
d’onda devono “piegarsi”, modificando la direzione di propagazione.
Interessante è pure il fatto
che a distinguere un mezzo
di propagazione dall’altro è la velocità di propagazione delle onde e, riferito
alla luce, questo deve avere a che fare con l’indice di rifrazione
Per quanto riguarda le onde
meccaniche, la rifrazione può essere osservata su un ondoscopio. Occorre
semplicemente trovare il modo per realizzare il passaggio di un’onda piana da un mezzo di propagazione ad
un altro. Si può ottenere, ad esempio, modificando la profondità
dell’acqua. Il risultato è quello che si osserva nel disegno a fianco. In acqua
bassa le onde vanno più piano e perciò, per garantire continuità al fronte
d’onda devono “piegarsi”, modificando la direzione di propagazione.
Interessante è pure il fatto
che a distinguere un mezzo
di propagazione dall’altro è la velocità di propagazione delle onde e, riferito
alla luce, questo deve avere a che fare con l’indice di rifrazione
 v sempre minore o uguale a c, la quale è la massima
velocità possibile (relatività di Einstein)
n è una proprietà fondamentale dei mezzi materiali
trasparenti (e più misurabile rispetto alla v!)
L’indice di rifrazione n può variare con la lunghezza
d’onda: onde luminose di lunghezza d’onda maggiore hanno n minore e viceversa.
(http://www00.unibg.it/dati/corsi/208406/6847-Lezione14.pdf)
Vediamo ora come
la teoria ondulatoria spiega il fenomeno della rifrazione della luce sulla base
del principio di Huygens. Costruiamo, quindi, il raggio rifratto con il
metodo dell'inviluppo piano.
Consideriamo due mezzi in cui la luce si propaga
rispettivamente con velocità v1 e v2 (per il momento
supponiamo v1>v2).
Consideriamo poi un'onda piana che si muove nel mezzo con
velocità v1, tre raggi d'onda e un fronte d'onda, AC, che comincia
ad incontrare la superficie di separazione dei due mezzi nel punto A.
v sempre minore o uguale a c, la quale è la massima
velocità possibile (relatività di Einstein)
n è una proprietà fondamentale dei mezzi materiali
trasparenti (e più misurabile rispetto alla v!)
L’indice di rifrazione n può variare con la lunghezza
d’onda: onde luminose di lunghezza d’onda maggiore hanno n minore e viceversa.
(http://www00.unibg.it/dati/corsi/208406/6847-Lezione14.pdf)
Vediamo ora come
la teoria ondulatoria spiega il fenomeno della rifrazione della luce sulla base
del principio di Huygens. Costruiamo, quindi, il raggio rifratto con il
metodo dell'inviluppo piano.
Consideriamo due mezzi in cui la luce si propaga
rispettivamente con velocità v1 e v2 (per il momento
supponiamo v1>v2).
Consideriamo poi un'onda piana che si muove nel mezzo con
velocità v1, tre raggi d'onda e un fronte d'onda, AC, che comincia
ad incontrare la superficie di separazione dei due mezzi nel punto A.

 Il punto A comincia ad emettere onde sferiche elementari che si propagano nel
secondo mezzo. Mentre queste onde avanzano, i restanti punti del fronte d'onda
continuano a viaggiare nel primo mezzo, incontrando la superficie di
separazione dei due mezzi in tempi successivi. Poiché le velocità di
propagazione sono diverse, le distanza percorse, a parità di tempi, saranno
diverse: quando il punto B raggiunge la superficie di separazione in B', l'onda
secondaria emessa da A avrà percorso un tratto di lunghezza inferiore a BB'.
Il punto A comincia ad emettere onde sferiche elementari che si propagano nel
secondo mezzo. Mentre queste onde avanzano, i restanti punti del fronte d'onda
continuano a viaggiare nel primo mezzo, incontrando la superficie di
separazione dei due mezzi in tempi successivi. Poiché le velocità di
propagazione sono diverse, le distanza percorse, a parità di tempi, saranno
diverse: quando il punto B raggiunge la superficie di separazione in B', l'onda
secondaria emessa da A avrà percorso un tratto di lunghezza inferiore a BB'.
 A questo punto anche B' comincia ad emettere onde, mentre l'onda emessa da A
continua ad avanzare, ed il punto C' del fronte d'onda viaggia, nel primo
mezzo, fino ad incontrare la superficie di separazione in C''. Quando C' sarà
arrivato in C'', le onde emesse da A e B' avranno l'aspetto in figura.
A questo punto anche B' comincia ad emettere onde, mentre l'onda emessa da A
continua ad avanzare, ed il punto C' del fronte d'onda viaggia, nel primo
mezzo, fino ad incontrare la superficie di separazione in C''. Quando C' sarà
arrivato in C'', le onde emesse da A e B' avranno l'aspetto in figura.
 Secondo il principio di Huygens la superficie d'onda rifratta sarà l'inviluppo di tutte le superfici d'onda
secondarie emesse dai punti che successivamente incontrano la superficie di
separazione tra i due mezzi. I raggi d'onda rifratti saranno perpendicolari al
fronte d'onda rifratto, come mostrato nella figura.
Allora l'inviluppo dopo il tempo Dt avrà
cambiato direzione di propagazione.
Non solo il modello ondulatorio prevede la rifrazione, ma da esso si
deduce pure la legge di Snell della rifrazione:
Secondo il principio di Huygens la superficie d'onda rifratta sarà l'inviluppo di tutte le superfici d'onda
secondarie emesse dai punti che successivamente incontrano la superficie di
separazione tra i due mezzi. I raggi d'onda rifratti saranno perpendicolari al
fronte d'onda rifratto, come mostrato nella figura.
Allora l'inviluppo dopo il tempo Dt avrà
cambiato direzione di propagazione.
Non solo il modello ondulatorio prevede la rifrazione, ma da esso si
deduce pure la legge di Snell della rifrazione:
 dove nr e ni sono le velocità del raggio nei mezzi r e i
raggio più lento → traiettoria più vicina alla normale (e
viceversa)
La frequenza dell’onda rimane invariata
La lunghezza d’onda diminuisce se n diminuisce, o aumenta
se n aumenta
dove nr e ni sono le velocità del raggio nei mezzi r e i
raggio più lento → traiettoria più vicina alla normale (e
viceversa)
La frequenza dell’onda rimane invariata
La lunghezza d’onda diminuisce se n diminuisce, o aumenta
se n aumenta