Resolución de sistemas de ecuaciones por el método gráfico
Palabras clave
Ecuaciones, sistema de ecuaciones, método gráfico, resolver una ecuación, solución de ecuaciones
¿Qué es un sistema de ecuaciones?
Un sistema de ecuaciones es un conjunto de ecuaciones que comparten por lo menos una
variable. La solución de un sistema de ecuaciones son los valores de las variables que hacen que cada una de las ecuaciones del sistema sea verdadera.
El número de soluciones de nuestro sistema dependerá de la ecuación de mayor grado. Por ejemplo, si tenemos un sistema formado por una ecuación lineal y otra cuadrática (grado dos), tendremos dos soluciones. Sin embargo, existen sistemas de ecuaciones que carecen de solución, o tienen infinitas soluciones.
Hay varios métodos para resolver un sistema de ecuaciones, tales como el de reducción,
igualación y sustitución, sin embargo, en esta hoja dinámica aprenderemos a resolverlas
por el método gráfico, utilizando las herramientas que nos proporciona Geogebra.
¿Cómo resolver un sistema de ecuaciones?

1. Escribimos nuestras dos ecuaciones en la barra de entrada. Una vez las hayamos escrito, aparecerán automáticamente en la vista algebraica y en la gráfica.
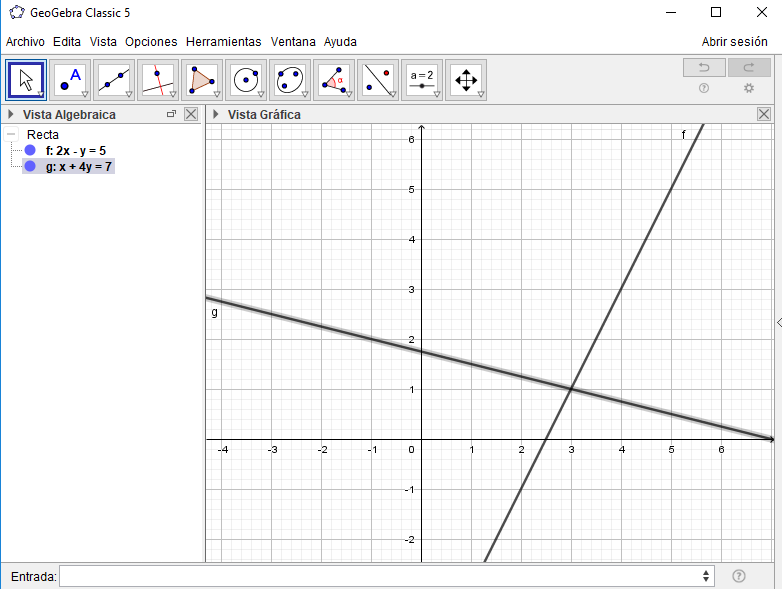
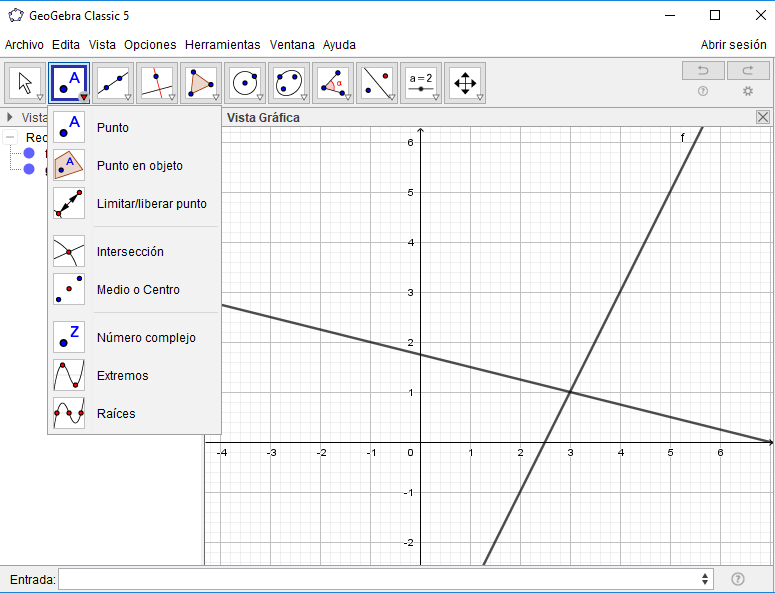
2. Luego, utilizaremos la herramienta Intersección, para obtener el punto en el que las dos rectas se cortan. Luego de haber elegido esta herramienta, seleccionaremos nuestras dos rectas, ya sea dándoles clic en la vista gráfica o en la algebraica.
3. El punto obtenido es justamente la solución de nuestro sistema de ecuaciones, dado por un par de coordenadas. En este caso, nuestra solución es (3,1), o sea, x=3; y=1.
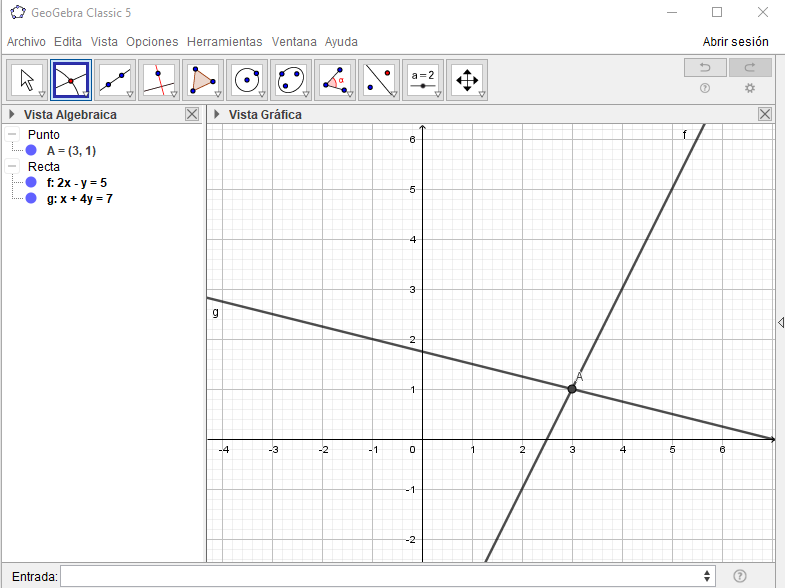
4. Por último, vamos a comprobar nuestro resultado, sustituyendo el valor de x e y en ambas ecuaciones.

Actividad 1. ¡Ahora es tu turno! Resuelve el siguiente sistema de ecuaciones a partir del método gráfico. Repasa los pasos del ejemplo anterior, y recuerda que el número de soluciones dependerá de la ecuación de mayor grado.
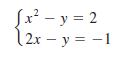
Comprueba tu respuesta
La respuesta obtenida en la actividad anterior fue:
Otra forma de realizar el método gráfico
Actividad 2.
Haz clic aquí para practicar esta otra forma del método gráfico.
Preguntas de repaso:
1. ¿Qué es un sistema de ecuaciones?
2. ¿Qué es la solución de un sistema de ecuaciones?
3. El método gráfico es la única forma de resolver un sistema de ecuaciones:
4. La solución de un sistema de ecuaciones nunca se expresa en forma de par de ordenado:
5. El punto (s) de intersección de las gráficas de las ecuaciones describen la solución (s) del sistema de ecuaciones:
Referencias bibiográficas:
Stewart, J., Redlin, J., & Watson, S. (2007). Precálculo.
Matemáticas para el cálculo (5ta ed.). Ciudad de México: Cengage Learning.