GeoA 4 4798
Δίνεται αμβλυγώνιο τρίγωνο ΑΒΓ με ΑΒ<ΑΓ και γωνία Α>90. Φέρνουμε τμήμα ΒΔ κάθετο στην ΑΒ και με ΒΔ=ΑΓ και τμήμα ΓΕ κάθετο στην ΑΓ με ΓΕ=ΑΒ.
Θεωρούμε τα μέσα Ζ και Θ των ΑΔ και ΑΕ καθώς και τη διχοτόμο Αδ της γωνίας ΔΑΕ.
α) Να αποδείξετε ότι ΑΔ=ΑΕ. (Μονάδες 9)
β) Αν Κ τυχαίο σημείο της διχοτόμου Αδ, να αποδείξετε ότι το Κ ισαπέχει από τα μέσα Ζ και Θ. (Μονάδες 9)
γ) Αν το Κ είναι σημείο της διχοτόμου Αδ τέτοιο ώστε ΚΖ=ΑΖ, να αποδείξετε ότι το τετράπλευρο ΑΖΚΘ είναι ρόμβος. (Μονάδες 7)
Απόδειξη
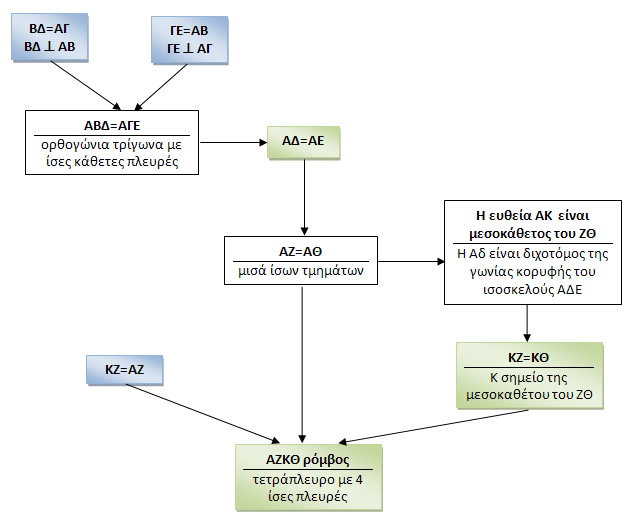
Χρησιμοποιείστε το παρακάτω διάγραμμα για να γράψετε την απόδειξη.