Buchinhalt in Kürze
Die ebene Möbiusgeometrie kann man auf verschiedene Weisen darstellen. Erweitert man die euklidische Ebene um einen weiteren Punkt , und betrachtet man die durch gehenden Geraden auch als "Kreise", so ergeben sich möbiusgeometrische Aussagen, wenn man die euklidischen Abbildungen um die Spiegelungen an Kreisen ergänzt. Eine wichtige möbiusgeometrische Invariante, nämlich das komplexe Doppelverhältnis von 4 Punkten, ist in der euklidischen Darstellung im jedoch nur schwer rechnerisch nutzbar.
Hierzu eignet sich besser die Darstellung in der Gauss'sche Zahlenebene. 4 Punkte liegen auf einem Kreis genau dann, wenn ihr Doppelverhältnis reell ist. Doch auch in dieser Darstellung stört die Sonderstellung der Geraden und es fehlt der Punkt . Von hier aus gibt es nun zwei Möglichkeiten der Erweiterung:
Die komplexe projektive Gerade erlaubt eine einheitliche Behandlung der "Punkte" und der "Kreise", sowie die Berechnung des Doppelverhältnisses. Kreise werden beschrieben als Nullstellen hermitescher Spiegelungen.
Die Gruppe der orientierungserhaltenden Möbiusabbildungen ist dann isomorph zu .
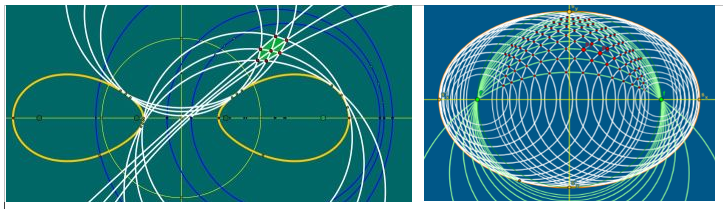
Die zweite mögliche Erweiterung liefert die stereographische Projektion: die Punkte der euklidischen, bzw. der Gauss'schen Zahlenebene werden auf eine Quadrik von Typ der Kugel projiziert. Kreise sind dann die ebenen Schnitte mit der Quadrik. Die Möbiusebene wird dabei dargestellt im reell 3-dimensionalen projektiven Raum mit einer Quadrik vom Typ der Kugel, dh. mit einer reellen quadratischen Form der Signatur (+,+,+,-). Die Gruppe der orientierungserhaltenden Möbiusabbildungen ist in dieser Darstellung isomorph zu .
Eine weitere Darstellung ergibt sich, wenn man in einer Art komplexen stereographischen Projektion die komplexe projektive Gerade auf einen nichtausgearteten Kegelschnitt in der komplexen projektiven Ebene projiziert: die Möbiusgruppe erweist sich dann als isomorph zu . Geometrisch durchsichtig erscheint diese Darstellung zunächst nicht.
Eine Deutung ergibt sich jedoch, wenn man den Geradenraum des Kugelmodells untersucht. Geraden, und damit die Kreisbüschel, können mit Hilfe der Plückerkoordinaten im reell 6-dimensionalen Geraden-Vektorraum dargestellt werden. Die mit der Möbiusquadrik gegebene Polarität erzeugt auf eine komplexe Struktur: wird zu einem komplexen Vektorraum mit einer nichtausgearteten komplexen quadratischen Form • . Zusätzlich besitzt gewissermaßen als komplexe Variante des Kreuzprodukts ein alternierendes Produkt [ , ] und erweist sich damit als Lie-Algebra der Möbiusgruppe. Die Vektoren des Geradenraums lassen in dieser Darstellung sehr vielfältige Deutungen zu:
- Geradenvektoren repräsentieren Kreisbüschel, das dazu orthogonale Kreisbüschel
- Vektoren allgemein sind infinitesimale Möbiusbewegungen. Sie erzeugen W-Bewegungen, das sind die nach Sophus Lie benannten Einparameter-Untergruppen der Möbiusgruppe. Deren Bahnkurven (W-Kurven) sind Kreisbüschel und ihre Isogonaltrajektorien (Loxodrome).
- Die isotropen Vektoren (für die gilt) repräsentieren Tangenten an die Möbiusquadrik und, projektiv betrachtet, die Punkte der Möbiusebene. Als Vektoren stellen sie infinitesimale parabolische Bewegungen dar. Sie können aber auch als Tangentialvektoren gedeutet werden. Damit kann man reelle sowie komplexe Kurven möbiusgeometrisch untersuchen, insbesondere ergibt sich ein möbius-geometrischer Zugang zur Funktionentheorie.
Im Geradenraum lässt sich die Lage von 4 Punkten einfach charakterisieren, sie kann mit der absoluten Möbiusinvariante von 4 Punkten beschrieben werden.
Lineare Vektorfelder auf der Möbiusquadrik gehören zu Kreisbüscheln und ihren Isogonal-Trajektorien.
Die Frage nach dem Ort, in welchem sich die Kreise zweier Kreisbüschel berühren, führt auf spezielle hermitesche Formen und ihren Lösungskurven, die sich als Cassini-Lemniskaten herausstellen. Allgemeiner sind diese Kurven der Ort, in welchem sich die Bahnkurven zweier verschiedener W-Bewegungen unter konstantem Winkel schneiden: wir haben es gewissermaßen mit der möbius-geometrischen Verallgemeinerung des Peripheriewinkelsatzes aus der euklidischen Geometrie zu tun!
Kreise und Kreisspiegelungen werden im Geradenraum durch involutorische hermitesche Abbildungen beschrieben. Zu ihnen gehören Unteralgebren der Lie-Algebra und als Untergeometrien die hyperbolische, bzw. die elliptische oder die euklidische Ebene.
Zu hermiteschen Abbildungen von gehören bizirkulare Quartiken. Das sind die Schnittkurven der Möbiusquadrik mit einer zweiten Quadrik. Neben den Kegelschnitten enthält diese Kurvenklasse einteilige und zweiteilige Quartiken mit 4 verschiedenen Brennpunkten. Die erwähnten Cassini-Lemniskaten sind Spezialfälle.
Quadratische Vektorfelder der Möbiusebene besitzen 4 Brennpunkte (Nullstellen). Die Integralkurven sind, falls die absolute Möbiusinvariante der 4 Brennpunkte reell ist, konfokale bizirkulare Quartiken. Sind die Brennpunkte verschieden, so beschreibt ein quadratisches Vektorfeld die Differentialgleichung einer elliptischen Funktion: .
Die absolute Invariante dieser elliptischen Funktion ist die absolute Möbiusinvariante der 4 Brennpunkte.
Die Untersuchung der bizirkularen Quartiken im Einzelnen ergibt, dass diese Kurven und ihre Eigenschaften die möbiusgeometrische Verallgemeinerung der Kegelschnitte sind: "Brennstrahlen" sind Brennkreise, die Kurven können mit Hilfe der Brennpunkte und den zugehörigen Leitkreisen „konstruiert“ werden. Sie lassen sich deuten als Überlagerung zweier Wellenbewegungen aus Kreisbüscheln.
Drei beliebige verschiedene Geradenbüschel in der Ebene erzeugen stets ein Sechseckgewebe.
Über Sechseckgewebe aus Geraden gibt der Satz von Graf und Sauer Auskunft: "Sechseckgewebe aus Geraden bestehen aus den Tangenten einer Kurve 3. Klasse". [GRA_SA]
Beispielsweise bilden die Tangenten einer gewöhnlichen Funktion 3. Ordnung ein solches Sechseckgewebe, ebenso die Normalen einer Parabel. Letztere hüllen eine Neil‘sche Parabel ein.
Die 1938 von W. Blaschke gestellte Frage nach allen Sechseckgeweben aus Kreisen ist möglicherweise noch unbeantwortet [BLA_BO]. Drei Kreisbüschel bilden nur in ganz speziellen Fällen ein Sechseckgewebe. Wir werden diese Fälle im Buch bestimmen und anzeigen. Bizirkulare Quartiken besitzen Scharen von doppelt-berührenden Kreisen. Wenn eine bizirkulare Quartik mehr als zwei verschiedene solche Scharen besitzt, so kann man aus diesen Scharen Sechseckgewebe erzeugen. Zum Beispiel kann man aus den Tangenten und den von außen doppelt berührenden Kreisen einer Ellipse Sechseckgewebe konstruieren.
Wir vermuten, dass ein Sechseckgewebe aus Kreisen, welches weder die Projektion eines gradlinigen Sechseckgewebe ist noch zu den oben genannten Geweben aus speziellen Kreisbüscheln gehört, aus doppelt-berührenden Kreisen einer bizirkularen Quartik besteht. (Stand: 2019)
Nachtrag: 2013 wurden neue Beispiele von hexagonalen Geweben aus Kreisen veröffentlicht, die obige Vermutung wohl widerlegen.
Siehe das Kapitel "Neue 6-Eck-Gewebe aus Kreisen".
Diese Seite ist Teil des GeoGebra-Books Moebiusebene.