Golden ratio
Definition
Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities.
By using the
LocusEquation[g/h==f/g,C] command one can find the approximate place of the golden cut of segment AB. (For technical reasons, if the locus is a zero dimensional object, then its algebraic equation contains some numerical approximations. If you zoom in the figure, you may find that the equation is changing on deeper zooming: its coefficients are usually bigger.)
By zooming out, surprisingly you will find another point at about -1.618 which also fulfills the criterion. Actually, GeoGebra's Automated Reasoning Tools, due to the mathematical background being used, always handles both irrational roots of a quadratic equation indistinguishly, so it is impossible to designate only one root of them.Constructing the golden ratio
The classic method to construct the golden ratio for a given segment AB is as shown below. Here we explicitly construct the length , assuming that AB=1. Now by typing
Relation[f/p,p/(f-p)] we can conclude that f/p is indeed the golden ratio of f.It makes sense to compare other expressions of f and p. For example, G must be the golden cut for the segment AH. Can you check this property by using the Relation command again?
Diagonals of a regular pentagon
It is well known that the proportion of a diagonal and a side of a regular pentagon is in the golden ratio. To check this, draw a regular pentagon with GeoGebra, create one of its diagonals, and check the proportion by using the Relation command. (Make sure you show the labels of the created objects by using the right click of the mouse. Then you can refer to the labels easily in the typed command.)
Pentagon in the pentagon, and so on
In the following figure (taken from a blog, but it can also be found in Jonathan Quintin's video The Golden Key from 1:40) you can find an idea to embed arbitrary many pentagons in a regular way.
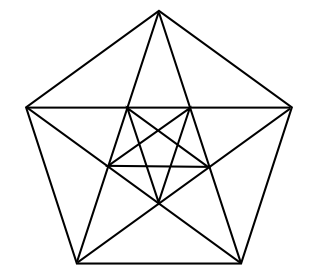
Construct this figure with GeoGebra and find equal long segments among the appearing ones. So you can directly derive further proportions which are again the golden ratio.
Finallly... the regular decagon
The golden ratio also appears in a combination of a regular pentagon and a regular decagon, having the same side lengths, as shown below.
Challenges
- Find golden cuts in the figure and confirm your conjectures by using GeoGebra Automated Reasoning Tools. You can create additional segments by using the appropriate tool if needed.
- Which property does the point L have? Confirm your conjecture.