Contour
Mike May Calculus
This is a collection of applets for single variable calculus.
It should grow as time goes on.
Let me know if you can think of demonstrations that should be added.
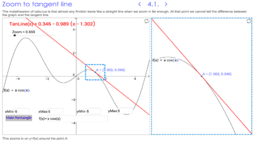
Table des matières
Overview
Chapter 1 Preliminary material
Chapter 2 Limits
Chapter 3 Derivatives conceptually
Chapter 4 Derivatives symbolically
Chapter 5 Applications of the derivative
- Chapter working notes
- Newton's Method
- Linearization and Linear Approximation Demonstration
- Linear (Tangent Line) Approximation
- Optimize area of side-by-side rectangular plots
- Optimization - Rowing and Running
- Section 2.8-Related Rates-Ladder Falling
- Related Rates - Square
- Slope Fields
- Parametric Curves and tangent line
Chapter 6 Integrals
Chapter 7 Applications of integration
Chapter 8 Series
Chapter 9 Differential Equations