Una semplice applicazione di trigonometria: i vettori
Senza conoscere ancora tutte le complesse regole della goniometria e delle trigonometria, possiamo già vedere un'applicazione molto utile per quello che abbiamo imparato sugli angoli: la gestione di grandezze vettoriali.
Ricordiamo che mentre una grandezza si dice "scalare" se è definita da un valore numerico (ad esempio un'età, un prezzo o la massa di un oggetto), le grandezze vettoriali descrivono fenomeni più complessi, e quindi hanno bisogno di più informazioni per essere definite. Vediamo questo concetto nella breve animazione qui sotto.
Una tecnica molto comune che si utilizza lavorando con le grandezze vettoriali è scomporle in componenti, cioè vederle come somma di vettori orientati in certe direzioni specifiche che sono particolarmente significative ed utili. Questa operazione, che è strettamente legata alla somma di vettori, è descritta nell'animazione seguente.
Iniziamo ad intuire la relazione che tutto questo ha con gli angoli e con la trigonometria: poiché un vettore e le sue componenti sono inclinati l'uno rispetto alle altre di un certo angolo, se vogliamo sapere la lunghezza di questi vettori (cioè il loro modulo) abbiamo bisogno di conoscere come si lavora con gli angoli.
Vediamo qui sotto un esempio in cui, dato un vettore di conosciamo il modulo (cioè la lunghezza), vogliamo calcolare il modulo di una delle sue componenti.
ATTENZIONE: in questo primo esempio NON usiamo esplicitamente i concetti di seno e coseno, ma ripercorriamo il ragionamento che ci ha permesso di trovare i valori goniometrici dell'angolo di 60°.
In questo modo l'animazione è comprensibile anche a chi non ha ancora affrontato alla goniometria, mentre per chi la sta studiando è un'occasione in più per notare il significato concreto di seno e coseno.
Ovviamente chi conosce la definizione di seno e coseno può procedere più speditamente. Riproduciamo qui sotto l'immagine dei vettori interessati ed utilizziamo i concetti di goniometria per ottenere lo stesso risultato.
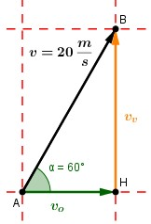
Poiché ci interessa , cioè il cateto opposto all'angolo , utilizziamo la definizione di seno:
da cui, ricavando :
Poiché in questo caso , sappiamo che il suo seno vale e quindi
che ovviamente coincide con il risultato ottenuto nell'animazione.
Se invece vogliamo trovare la componente orizzontale, notiamo che essa è il cateto adiacente all'angolo , e quindi dovremo fare riferimento alla definizione di coseno:
da cui, ricavando :
che, sostituendo , ci porta a
Puoi notare che abbiamo sostituito il valore di o solo al termine del ragionamento: conoscendo la definizione generale di seno e coseno si può risolvere il problema avendo un qualsiasi angolo , il cui seno sarà poi calcolato in vari modi possibili: ad esempio se è l'arco associato di un angolo noto, oppure attraverso le formule goniometriche (somma, duplicazione, bisezione, etc.) oppure, nel peggiore dei casi, utilizzando la calcolatrice.