Esquema
barycentrische coördinaten
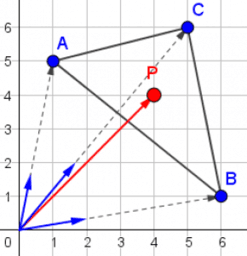
Je kunt de ligging van een punt beschrijven door een coördinatensysteem te gebruiken. In een cartesisch coördinatensysteem wordt de ligging van een punt bepaald als een lineaire combinatie van eenheidsvectoren op de coördinaatsassen. In polaire notatie wordt een punt bepaald door zijn afstand tot de oorsprong en een rotatiehoek, gemeten vanaf de x-as. Maar deze twee systemen zijn niet de enig mogelijke. In driehoeken kan je duizenden merkwaardige punten bepalen, die we driehoekscentra noemen. Hierbij is het handig om de hoekpunten van de driehoek als referentiepunten te nemen. Deze hoekpunten bepalen eenduidig de zogenaamde barycentrische coördinaten van een willekeurig punt t.o.v. deze driehoek.
In dit GeoGebraboek leer je meer over dit coördinatensysteem.