Rectangular to Polar Wrapping/Unwrapping
How does the function y = f(x) in rectangular coordinates relate graphically to the curve r = f(theta) in polar coordinates?
I recall trying to explain to my Calculus class last year how one may envision taking the rectangular function (or more specifically, its inverse) and wrapping it around a pole at the origin. Clearly my explanation fell short on many students.
This Geogebra construction is intended to demonstrate that concept.
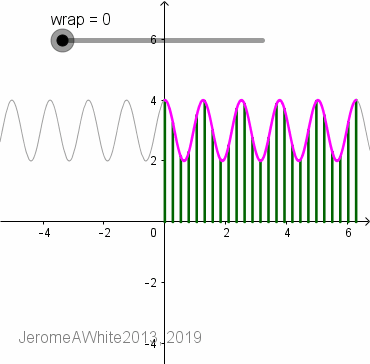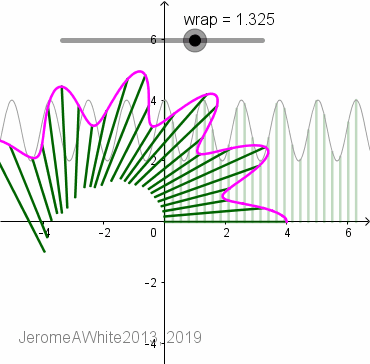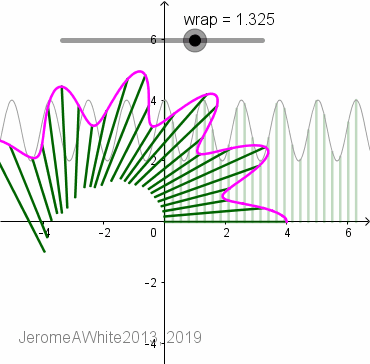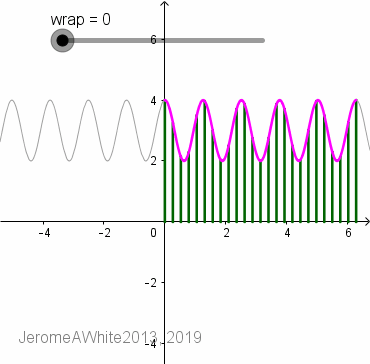
Drag the "wrap" slider left to right to see the function flip across y=x to display its inverse and then proceed to wrap around the pole.
Dynamically drag the original function (gray graph) up and down, left and right, and notice how the polar graph transforms accordingly.
Alternately, enter your own function into the f(x) box.