Ejercicio 14. Teorema de pitágoras

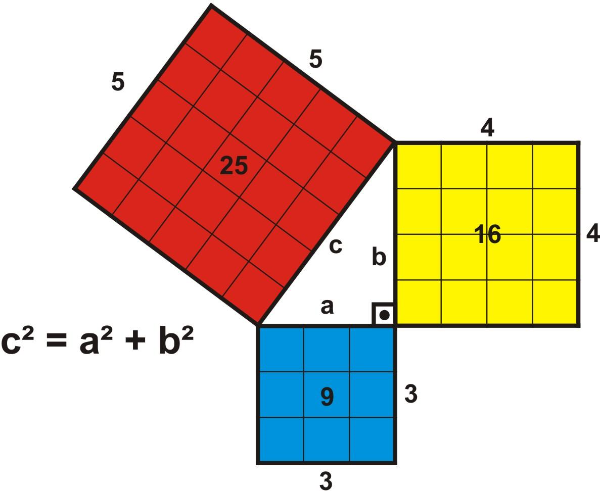
Teorema de Pitágoras Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos:

Si el triángulo tiene un ángulo recto (90°)... ... y pones un cuadrado sobre cada uno de sus lados, entonces...

... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!

El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es: En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²): a² + b² = c²

¿Seguro... ?Veamos si funciona con un ejemplo. Un triángulo de lados "3,4,5" tiene un ángulo recto, así que la fórmula debería funcionar

Veamos si las áreas son la misma: 3² + 4² = 5² Calculando obtenemos: 9 + 16 = 25 ¡sí, funciona!

Ejercicio 14. Teorema de pitágoras

Nuevos recursos

Descubrir recursos

Descubre temas