Integral calculus - determining areas
Let us go ahead to grade 12. At this grade Austrian students learn to work with the integral calculus. At grade 11 the have already learned to use the differential calculus.
In our math lessons we often start the integral calculus with the problem of calculating a curved area.
The following Applet shows the map of a city, where an area should be redesigned.
Curves Areas
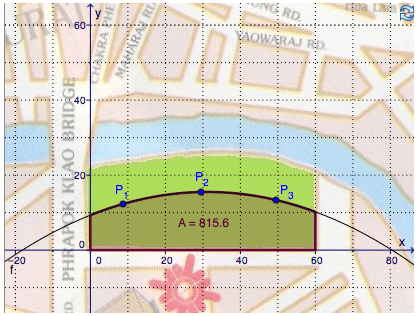
In this case students should only drag the points to get an area like the riverside. As you can see a function goes through this points. And the measurement of this area is shown by the applet. This Applet may lead to curiosity and the question:
• How does it work? How can we calculate areas like this?
Furthermore this applet animates students to demand reasoning – Level 1
Remember: By computing the area of circle we have used the idea of approximation. Now we use it again – according to the spiral curriculum we revisit this idea on higher level of content.
So in math lessons we now have to develop the idea of the lower sum and upper sum to calculate a curved area. We make rectangles that inscribe and circumscribe the curve.
Calculating curved areas
Level 1 - Disposition
Calculating the piece of a land
By making more rectangles the approximation is getting better. In the limit the upper and lower sum converge to a single value – the area under the curve.
Both applets show, how a curved area can be calculated with upper and lower sum.
Both applets are situated on Level 2. They foster the comprehension and the ability to understand and explain prescribed reasons.
Level 2 - Comprehension
Upper and lower sum 1
Upper an Lower sum 2
Level 2 and Level 3 - Comprehension and Communication
Fundamental Theorem of Calculus 1
Fundamental Theorem of Calculus 2
Step by step they handle the proof and the applets fosters the comprehension of this proof. Therefore this applet is located on Level 2. But it can also be used for explaining and arguing the completed mathematical proof. And than it belongs to Level 3.