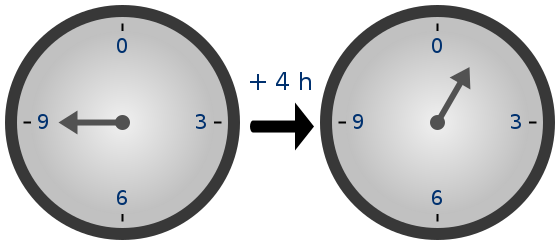
Ejercicio 13. Ejemplo de aritmética modular
- Tema:
- Aritmética
Aritmética modular
. En matemática, la aritmética modular es un sistema aritmético para clases de equivalencia de números enteros llamadas clases de congruencia. La aritmética modular fue introducida en 1801 por Carl Friedrich Gauss . Algunas veces se le llama, sugerentemente, aritmética del reloj, ya que los números «dan la vuelta» tras alcanzar cierto valor llamado módulo.Relación de congruencia.
La aritmética modular puede ser construida matemáticamente mediante la relación de congruencia entre enteros, que es compatible con las operaciones en el anillo de enteros: suma y multiplicación. Para un determinado módulo n, ésta se define de la siguiente manera: a y b se encuentran en la misma "clase de congruencia" módulo n, si ambos dejan el mismo resto si los dividimos entre n, o, equivalentemente, si a − b es un múltiplo de n. Esta relación se puede expresar cómodamente utilizando la notación de Gauss:{\displaystyle a\equiv b\ {\pmod {n}}}
Así se tiene por ejemplo
{\displaystyle 63\equiv 83\ {\pmod {10}}}
ya que ambos, 63 y 83 dejan el mismo resto (3) al dividir entre 10, o, equivalentemente, 63 − 83 es un múltiplo de 10. Se lee:
«63 es congruente con 83, módulo 10», «en módulo 10, 63 y 83 son congruentes», o «63 y 83 son congruentes uno con otro, módulo 10».
«Módulo» a veces se abrevia con la palabra «mod» al hablar, de la misma manera que como está escrito y proviene de la palabra modulus del latín, la lengua de los escritos originales de Gauss. Así, el número n, que en este ejemplo es 10, sería el modulus.
Otro ejemplo; cuando el módulo es 12, entonces cualesquiera dos números que divididos entre doce den el mismo resto son equivalentes (o "congruentes") uno con otro. Los números
..., −34, −22, −10, 14, 26,...son todos "congruentes módulo 12" unos con otros, ya que cada uno deja el mismo resto (2) cuando los dividimos entre 12. La colección de todos esos números es una clase de congruencia
